Problem 2751 Robot Collisions
Table of Contents
Problem Statement
Link - Problem 2751
Question
There are n 1-indexed robots, each having a position on a line, health, and movement direction.
You are given 0-indexed integer arrays positions, healths, and a string directions (directions[i] is either ‘L’ for left or ‘R’ for right).
All integers in positions are unique.
All robots start moving on the line simultaneously at the same speed in their given directions. If two robots ever share the same position while moving, they will collide.
If two robots collide, the robot with lower health is removed from the line, and the health of the other robot decreases by one. The surviving robot continues in the same direction it was going. If both robots have the same health, they are both removed from the line.
Your task is to determine the health of the robots that survive the collisions, in the same order that the robots were given, i.e. final heath of robot 1 (if survived), final health of robot 2 (if survived), and so on. If there are no survivors, return an empty array.
Return an array containing the health of the remaining robots (in the order they were given in the input), after no further collisions can occur.
Note: The positions may be unsorted.
Example 1
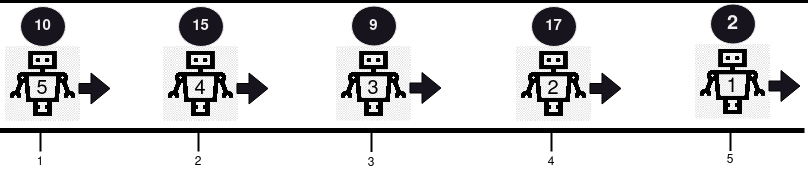
Input: positions = [5,4,3,2,1], healths = [2,17,9,15,10], directions = "RRRRR"
Output: [2,17,9,15,10]
Explanation: No collision occurs in this example,
since all robots are moving in the same direction.
So, the health of the robots in order from the first robot is returned,
[2, 17, 9, 15, 10].
Example 2
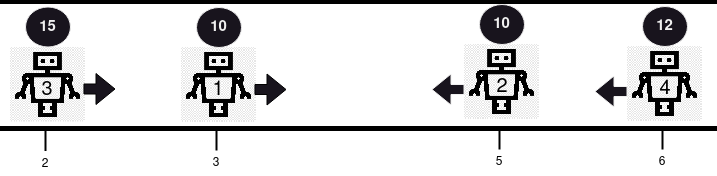
Input: positions = [3,5,2,6], healths = [10,10,15,12], directions = "RLRL"
Output: [14]
Explanation: There are 2 collisions in this example.
Firstly, robot 1 and robot 2 will collide, and since both have the same health,
they will be removed from the line.
Next, robot 3 and robot 4 will collide and since robot 4's health is smaller,
it gets removed, and robot 3's health becomes 15 - 1 = 14. Only robot 3 remains, so we return [14].
Example 3

Input: positions = [1,2,5,6], healths = [10,10,11,11], directions = "RLRL"
Output: []
Explanation: Robot 1 and robot 2 will collide and since both have the same health, they are both removed.
Robot 3 and 4 will collide and since both have the same health, they are both removed.
So, we return an empty array, [].
Constraints
- `1 <= positions.length == healths.length == directions.length == n <= 10^5`
- `1 <= positions[i], healths[i] <= 10^9`
- `directions[i] == 'L' or directions[i] == 'R'`
- All values in `positions` are distinct
Solution
class Solution {
public:
vector<int> survivedRobotsHealths(vector<int>& positions, vector<int>& healths, string directions) {
int size = positions.size();
vector<int>indices(size), result;
stack<int>st;
for(int ind = 0; ind<size; ind++){
indices[ind] = ind;
}
sort(indices.begin(), indices.end(),[&](int lhs, int rhs) { return positions[lhs] < positions[rhs]; });
for(int currInd:indices){
if(directions[currInd] == 'R'){
st.push(currInd);
}
else{
int topInd;
while(!st.empty() && healths[currInd]>0){
topInd = st.top();
st.pop();
if(healths[currInd]> healths[topInd]){
healths[currInd] -=1;
healths[topInd] = 0;
}
else if(healths[currInd]<healths[topInd]){
healths[currInd] = 0;
healths[topInd]-=1;
st.push(topInd);
}
else{
healths[currInd] = 0;
healths[topInd] = 0;
}
}
}
}
for(int ind = 0; ind<size; ind++){
if(healths[ind]>0){
result.push_back(healths[ind]);
}
}
return result;
}
};
Complexity Analysis
Time Complexity: O(nlogn)Space Complexity: O(n)
Explanation
1. Intuition
- Given the problem we can make the following observations.
1. A right going robot will never collide with another right going robot.
2. A left going robot will never collide with another left going robot.
3. A right going robot will collide with a left going robot only if the left going robot is to the right of the right going robot.
- Based on the above observations we can sort the robots based on their positions.
- Sorted array will contain the robots in the order which they are placed on the line.
- Now we can iterate over the sorted array and simulate the collisions.
- We need to calculate the collisions only between right and left going robots.
- We can use a stack to store the right going robots.
- If a left going robot is encountered we can check if there are any right going robots in the stack.
- If there are right going robots in the stack we can simulate the collision.
- If the left going robot has more health than the right going robot
we can reduce the health of the left going robot by 1.
- If the left going robot has less health than the right going robot
we can reduce the health of the right going robot by 1.
- If both the robots have the same health we can remove both the robots.
- We can continue this process until we reach the end of the sorted array.
- Finally, we can return the health of the robots that survived the collisions.
2. Implementation
- Initialize a vector `indices` of `size = positions.size()` to store the order of the robots.
- Initialize a stack `st` to store the positions of the right going robots.
- Sort the `indices` based on the positions of the robots.
- Iterate over the `indices` array.
- Assign the current index to `currInd`.
- If the current robot is right going push the `currInd` to the stack.
- Else do
1. While `st` is not empty and `healths[currInd]` is greater than 0.
- Pop the top index from the stack and assign it to `topInd`.
- If `healths[currInd]` is greater than `healths[topInd]`
reduce the health of `currInd` by 1 and set the health of `topInd` to 0.
- If `healths[currInd]` is less than `healths[topInd]`
reduce the health of `topInd` by 1,set the health of `currInd` to 0 and push the `topInd` to the stack.
This shows that 'right going robot is still alive'.
- If `healths[currInd]` is equal to `healths[topInd]` set the health of both `currInd` and `topInd` to 0.
- Iterate over the `healths` array and push the health of the robots that survived the collisions to the `result` array.
- Return the `result` array.
The above method will preserve the initial order of the robots.
Note -
The key point was to figure out the fact that the robots will collide only if they are moving in opposite directions and the left going robot is to the right of the right going robot. Also this fact can be used to sort the robots based on their positions and simulate the collisions.