Problem 1530 Number of Good Leaf Nodes Pairs
Table of Contents
Problem Statement
Link - Problem 1530
Question
You are given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.
Return the number of good leaf node pairs in the tree.
Example 1
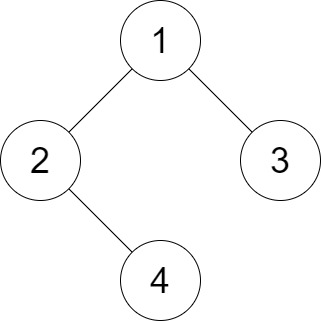
Input: root = [1,2,3,null,4], distance = 3
Output: 1
Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3.
This is the only good pair.
Example 2
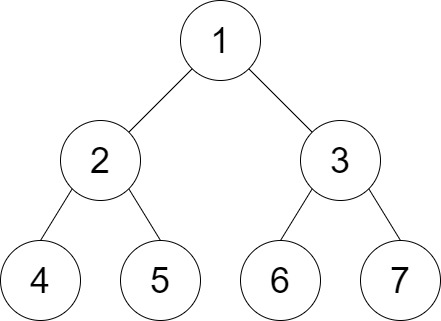
Input: root = [1,2,3,4,5,6,7], distance = 3
Output: 2
Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2.
The pair [4,6] is not good because the length of ther shortest path between them is 4.
Example 3
Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
Output: 1
Explanation: The only good pair is [2,5].
Constraints
- The number of nodes in the tree is in the range `[1, 2^10]`.
- `1 <= Node.val <= 100`
- `1 <= distance <= 10`
Solution
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int>countPair(TreeNode* root, int& dist, int& count){
if(!root)
return {0};
if(root->left == nullptr && root->right == nullptr)
return {1};
vector<int> left = countPair(root->left,dist,count);
vector<int> right = countPair(root->right,dist,count);
for(int i:left){
for(int j:right){
if(i>0 && j>0 && i+j<=dist){
count++;
}
}
}
vector<int>ans;
for(int i:left)
if(i>0 && i<dist)
ans.push_back(i+1);
for(int j:right)
if(j>0 && j<dist)
ans.push_back(j+1);
return ans;
}
int countPairs(TreeNode* root, int distance) {
int count = 0;
countPair(root,distance,count);
return count;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| DFS | O(n^2) | O(n) |
Explanation
1. Intuition
- We can count a good pair by checking the distance between the leaf nodes.
- We need to build up the distance calculations from the leaf nodes to the root.
- We can use a recursive approach to solve this problem.
- If we can track the distances from leaf nodes to the current node,
we can find out the combinations that match in that subtree
- Return 1 if the node is a leaf node.
- Return 0 if the node is null.
- Keep track of the distances of the leaf nodes from left subtree of current node,
and right subtree of the current node.
- Now we can find out the good pairs by checking the distances of the leaf nodes in the left subtree
and right subtree of the current node.
- If the sum of the distances of the leaf nodes in the left subtree and right subtree is less than or equal to the distance,
then we can increment the count.
- We can return the distances of the leaf nodes from the current node to the parent node.
2. Implementation
- Define a helper function `countPair` which takes the root node, distance and count as arguments.
- If the root is null, return a vector with 0.
- If the root is a leaf node, return a vector with 1.
- Recursively call the function on the left and right child of the current node.
- Store the distances of the leaf nodes of left subtree in the vector `left`.
- Store the distances of the leaf nodes of right subtree in the vector `right`.
- For each distance in the `left` vector,
- For each distance in the `right` vector,
- If the sum of the distances is less than or equal to the distance,
increment the count.
- Declare a vector `ans` to store the distances of the leaf nodes from the current node to the parent node.
- For each distance in the `left` vector,
- If the distance is greater than 0 and less than the distance,
add the distance + 1 to the `ans` vector.
- For each distance in the `right` vector,
- If the distance is greater than 0 and less than the distance,
add the distance + 1 to the `ans` vector.
- This adding `1` basically says that there is a node between the leaf node and the parent node.
- Return the `ans` vector.
This is a good problem to understand the concept of DFS and how we can use it to solve problems related to binary trees.