Posts

Problem 1823 Find the Winner of the Circular Game

Posted on Jul 9, 2024 5 mins

Table of Contents

Problem Statement

Question

There are n friends that are playing a game. The friends are sitting in a circle and are numbered from 1 to n in clockwise order. More formally, moving clockwise from the ith friend brings you to the (i+1)th friend for 1 <= i < n, and moving clockwise from the nth friend brings you to the 1st friend.

The rules of the game are as follows:

Start at the 1st friend.
Count the next k friends in the clockwise direction including the friend you started at. The counting wraps around the circle and may count some friends more than once.
The last friend you counted leaves the circle and loses the game.
If there is still more than one friend in the circle, go back to step 2 starting from the friend immediately clockwise of the friend who just lost and repeat.
Else, the last friend in the circle wins the game.
Given the number of friends, n, and an integer k, return the winner of the game.

Note

This is exactly the same as the Josephus problem, but with a different name. It is also called the n-people game.

Example 1

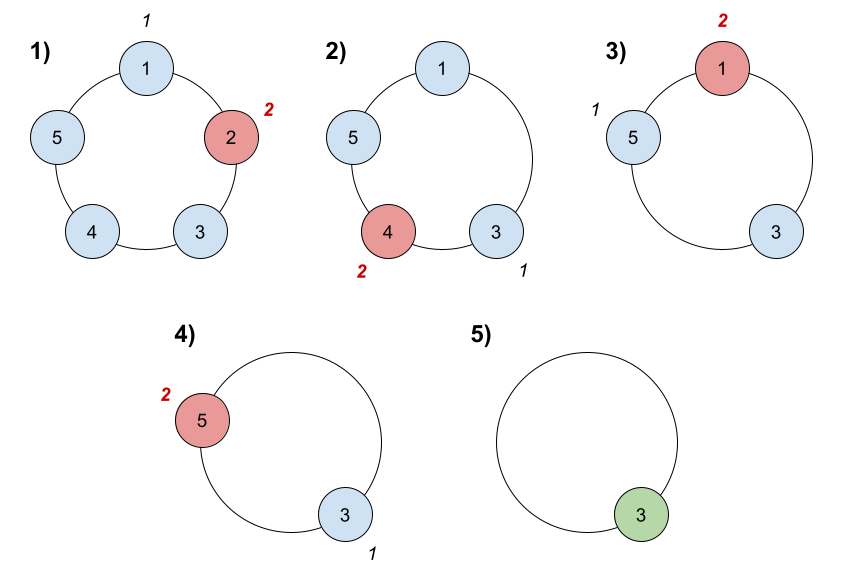
Simulation

Input: n = 5, k = 2
Output: 3
Explanation: Here are the steps of the game:

1. Start at friend 1.
2. Count 2 friends clockwise, which are friends 1 and 2.
3. Friend 2 leaves the circle. Next start is friend 3.
4. Count 2 friends clockwise, which are friends 3 and 4.
5. Friend 4 leaves the circle. Next start is friend 5.
6. Count 2 friends clockwise, which are friends 5 and 1.
7. Friend 1 leaves the circle. Next start is friend 3.
8. Count 2 friends clockwise, which are friends 3 and 5.
9. Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.

Example 2

Input: n = 6, k = 5
Output: 1
Explanation: The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.

Constraints

- `1 <= k <= n <= 500`

Solution

class Solution {
public:
    int findTheWinner(int N, int k) {

    int i = 1, ans = 0;

    while (i <= N) {
        ans = (ans + k) % i;
        i++;
    }
    return ans + 1;

    }
};

Complexity Analysis

Time Complexity : O(N)
Space Complexity : (1)

Explanation

1. Intuition

- We know that we can find the winner by simulating the result of each round from 1 to N.
- We will count `k` friends in the clockwise direction including the friend we started at.
- The quantity `ans` will store the index of the winner of each round.
- We will return the winner of the last round.
- The value `(ans+k)%i` will give us the index of the winner of the next round.
- How does it give the index of winner ?
  - Let's say we have `i` friends and we are at the `jth` friend.
  - We need to find the index of the winner of the next round.
  - We know that the winner of the next round will be the winner of the current round plus `k` friends.
  - but since the friends are being removed from the circle, we need to take the modulo of the number of friends got removed.
  - This will give us how many indexes we need to move from the current index to get the winner of the next round.

TLDR

- When there are n people, the person leaving is (k-1) positions away from the current starting person.
- The new starting position is the next person clockwise after the person who leaves.
- The winner for n people can be found using the winner of n-1 people adjusted by the counting step k.
- Don't forget to re-index to 1-indexing. Add 1 to the final answer.

2. Implementation

- Initialize the variables `i` and `ans` to 1 and 0 respectively.
- Iterate from 1 to N.
- Update the value of `ans` to `(ans+k)%i`.
- Return the value of `ans+1`.

Alternate Approach

class Solution {
public:
    int findTheWinner(int n, int k) {
        // Initialize vector of N friends, labeled from 1-N
        vector<int> circle;
        for (int i = 1; i <= n; i++) {
            circle.push_back(i);
        }

        // Maintain the index of the friend to start the count on
        int startIndex = 0;

        // Perform eliminations while there is more than 1 friend left
        while (circle.size() > 1) {
            // Calculate the index of the friend to be removed
            int removalIndex = (startIndex + k - 1) % circle.size();

            // Erase the friend at removalIndex
            circle.erase(circle.begin() + removalIndex);

            // Update startIndex for the next round
            startIndex = removalIndex;
        }

        return circle.front();
    }
};

Time Complexity: O(N^2)
Space Complexity: O(N)

Explanation

- Just simulate the game by removing the friends one by one.
- Keep track of the index of the friend to start the count on.
- Calculate the index of the friend to be removed.
- Erase the friend at the removal index.
- Update the startIndex for the next round.
- Return the winner of the game.