Problem 1110 Delete Nodes and Return Forest
Table of Contents
Problem Statement
Link - Problem 1110
Question
Given the root of a binary tree, each node in the tree has a distinct value.
After deleting all nodes with a value in to_delete, we are left with a forest (a disjoint union of trees).
Return the roots of the trees in the remaining forest. You may return the result in any order.
Example 1
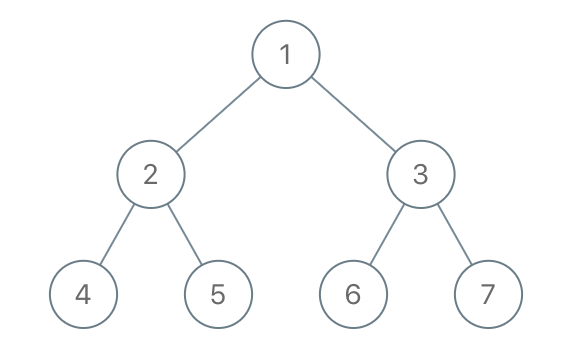
Input: root = [1,2,3,4,5,6,7], to_delete = [3,5]
Output: [[1,2,null,4],[6],[7]]
Example 2
Input: root = [1,2,4,null,3], to_delete = [3]
Output: [[1,2,4]]
Constraints
- The number of nodes in the given tree is at most `1000`.
- Each node has a distinct value between `1` and `1000`.
- `to_delete.length <= 1000`
- `to_delete` contains distinct values between `1` and `1000`.
Solution
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void delNode(TreeNode* &root, vector<bool>& todel, vector<TreeNode*>& result){
if(root != nullptr){
delNode(root->left,todel,result);
delNode(root->right,todel,result);
if(todel[root->val] == true){
if(root->left)
result.push_back(root->left);
if(root->right)
result.push_back(root->right);
root = nullptr;
}
}
else
return;
}
vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
vector<bool>todel(1001,false);
for(const auto it:to_delete)
todel[it] = true;
vector<TreeNode*>res;
delNode(root,todel,res);
if(root)
res.push_back(root);
return res;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| DFS | O(n) | O(n) |
Explanation
1. Intuition
- We can recursively traverse the tree and delete the nodes which are present in the `to_delete` vector.
- Once we delete the node, we can add the left and right child of the node to the result vector.
- But this pruning should be done in a post-order traversal so that
we can delete nodes from the leaf nodes back to root.
2. Implementation
- Since we know that the values of the nodes are distinct, we can use a vector of size 1001 to store the nodes to delete.
- Declare a vector `toDel` of size 1001 and initialize it to false.
- For each value in the `to_delete` vector, set the value at that index to true.
- Declare a vector of TreeNode `res` to store the result.
- Call the `delNode` function with the root, `toDel`, and `res` as arguments.
- Helper function `delNode`:
- If the root is not null, recursively call the function on the left and right child.
- If the value of the root is present in the `toDel` vector, add the left and right child to the result vector and set the root to null.
- once the `delNode` function is called, check if the root is not null and add it to the result vector.
- Return the result vector.