• Posts

Problem 3286 Find a Safe Walk Through a Grid

Problem Statement

Link - Problem 3286

Question

You are given an m x n binary matrix grid and an integer health.

You start on the upper-left corner (0, 0) and would like to get to the lower-right corner (m - 1, n - 1). You can move up, down, left, or right from one cell to another adjacent cell as long as your health remains positive.

• Cells (i, j) with grid[i][j] = 1 are considered unsafe and reduce your health by 1.

Return true if you can reach the final cell with a health value of 1 or more, and false otherwise.

Example 1

Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]], health = 1

Output: true

Explanation:
The final cell can be reached safely by walking along the gray cells below.

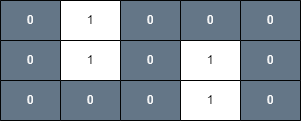
Example 2

Input: grid = [[0,1,1,0,0,0],[1,0,1,0,0,0],[0,1,1,1,0,1],[0,0,1,0,1,0]], health = 3

Output: false

Explanation:
A minimum of 4 health points is needed to reach the final cell safely.

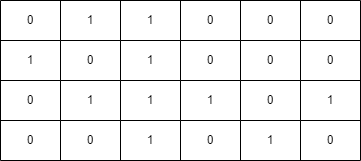
Example 3

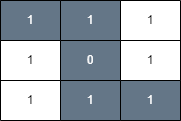
Input: grid = [[1,1,1],[1,0,1],[1,1,1]], health = 5

Output: true

Explanation:
The final cell can be reached safely by walking along the gray cells below.
Any path that does not go through the cell (1, 1) is unsafe
since your health will drop to 0 when reaching the final cell.

Constraints

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• 2 <= m * n
• 1 <= health <= m + n
• grid[i][j] is either 0 or 1.

Solution

class Solution {
public:
    bool findSafeWalk(vector<vector<int>>& grid, int health) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, -1));
        dp[0][0] = health - grid[0][0];

        queue<pair<int, int>> q;
        q.push({0, 0});

        vector<int> dirX = {1, -1, 0, 0};
        vector<int> dirY = {0, 0, 1, -1};

        while (!q.empty()) {
            auto [x, y] = q.front();
            q.pop();

            for (int i = 0; i < 4; ++i) {
                int newX = x + dirX[i], newY = y + dirY[i];
                if (newX >= 0 && newX < m && newY >= 0 && newY < n) {
                    int nheal = dp[x][y] - grid[newX][newY];
                    if (nheal > dp[newX][newY]) {
                        dp[newX][newY] = nheal;
                        if (nheal > 0) {
                            q.push({newX, newY});
                        }
                    }
                }
            }
        }
       // for(int i=0;i<m;i++){
         //   for(int j = 0; j<n ; j++){
           //       cout<<dp[i][j]<<" ";
            //}
            //cout<<endl;
        //}
        return dp[m-1][n-1] > 0;
    }
};

Complexity Analysis

| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| BFS       | O(mn)           | O(mn)            |

Explanation

1. Intuition

• Since this is a path finding problem, we would need BFS or DFS to find the path.
• We can use BFS to find the path from the start to the end.
• To keep track of health we can make use of a 2D dp array, where dp[x][y] would store the health at cell (x, y).
• Edge cases are
  • If the health at the start is less than 1, then we cannot reach the end.
  • If the starting cell is unsafe, we need to reduce the health by 1 before starting the traversal.
• Use a queue to store the cells to be traversed.
• Push (0, 0) to the queue and start the traversal.
• For each cell, find the health at the adjacent cells in all valid directions.
  • if the health adjacent cell is greater than the health in dp array, update the health in dp array and push the cell to the queue.
  • Continue this process until the queue is empty.
• Return the health at the end cell and check if it is greater than 0.

2. Implementation

- Initialize a 2D vector `dp` of size `m x n` with -1.
- Set the health at the starting cell to `health - grid[0][0]`.
- Initialize a queue `q` to store the cells to be traversed.
- Push the starting cell (0, 0) to the queue.
- Initialize two vectors `dirX` and `dirY` to store the directions.
- While queue is not empty,
  - Pop the front cell from the queue.
  - For each direction, if the cell is valid
    - Calculate the health at the adjacent cell as `dp[x][y] - grid[newX][newY]`.
    - If the health at the adjacent cell is greater than the health in dp array, update the health in dp array.
    - If the health at the adjacent cell is greater than 0, push the cell to the queue.
- Return the health at the end cell and check if it is greater than 0.