Problem 885 Spiral Matrix III
Table of Contents
Problem Statement
Link - Problem 885
Question
You start at the cell (rStart, cStart) of an rows x cols grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.
You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid's boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all rows * cols spaces of the grid.
Return an array of coordinates representing the positions of the grid in the order you visited them.
Example 1:
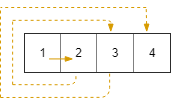
Input: rows = 1, cols = 4, rStart = 0, cStart = 0 Output: [[0,0],[0,1],[0,2],[0,3]]
Example 2:
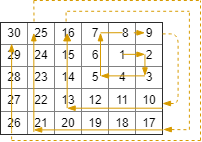
Input: rows = 5, cols = 6, rStart = 1, cStart = 4 Output: [[1,4],[1,5],[2,5],[2,4], [2,3],[1,3],[0,3],[0,4], [0,5],[3,5],[3,4],[3,3], [3,2],[2,2],[1,2],[0,2], [4,5],[4,4],[4,3],[4,2], [4,1],[3,1],[2,1],[1,1], [0,1],[4,0],[3,0],[2,0], [1,0],[0,0]]
Constraints:
1 <= rows, cols <= 1000 <= rStart < rows0 <= cStart < cols
Solution
class Solution {
public:
vector<vector<int>> spiralMatrixIII(int rows, int cols, int rStart, int cStart) {
vector<vector<int>> directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // East, South, West, North
vector<vector<int>> result = {{rStart, cStart}};
int steps = 0, d = 0;
while (result.size() < rows * cols) {
if (d == 0 || d == 2) steps++;
for (int i = 0; i < steps; i++) {
rStart += directions[d][0];
cStart += directions[d][1];
if (rStart >= 0 && rStart < rows && cStart >= 0 && cStart < cols) {
result.push_back({rStart, cStart});
}
if (result.size() == rows * cols) return result;
}
d = (d + 1) % 4;
}
return result;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| ----------------------- | --------------- | ---------------- |
| Spiral Matrix Traversal | O(rows cols) | O(rows cols) |
Explanation
Intial Thoughts
To approach this problem, consider the spiral path as a series of connected line segments that turn right at each corner. The key is to track the number of steps taken in each direction and the current direction. Initially, think about the grid as a cartesian plane and visualize how the spiral would unfold. The given code defines four directions: east, south, west, and north, which corresponds to moving right, down, left, and up in the grid. Start by identifying the current position and the total number of steps required to visit every cell in the grid.
Intuitive Analysis
Intuitively, to solve this problem, think about the spiral path as layers of concentric rectangles, where each layer represents a part of the spiral that can fit within the grid. Each layer consists of four line segments, and the number of steps in each segment increases by one after every four turns. The solution iterates through the grid, adjusting the direction and steps as necessary, ensuring that it visits every cell exactly once. Consider visualizing the grid with the given start and end points and imagine tracing the spiral path to better understand the problem’s solution.
1. Intuition
- The problem requires traversing a grid in a clockwise spiral order, starting from a given cell.
- To achieve this, we need to keep track of the current direction and the number of steps to take in that direction.
- The spiral pattern can be divided into four directions: east, south, west, and north, which can be represented by the
directionsarray. - We need to increase the number of steps every two directions to maintain the spiral pattern.
- The key insight is to check if the current cell is within the grid boundaries before adding it to the result.
- The algorithm should continue until all cells in the grid have been visited.
- The use of the modulo operator (
%) ensures that the direction index wraps around to the start of thedirectionsarray.
2. Implementation
- The
directionsarray is defined as{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}to represent the four directions. - The
stepsvariable is used to keep track of the number of steps to take in the current direction, and is incremented every two directions. - The
dvariable is used as an index into thedirectionsarray to determine the current direction. - The line
rStart += directions[d][0]; cStart += directions[d][1];updates the current cell coordinates based on the current direction. - The conditional statement
if (rStart >= 0 && rStart < rows && cStart >= 0 && cStart < cols)checks if the current cell is within the grid boundaries. - The line
result.push_back({rStart, cStart});adds the current cell to the result if it is within the grid boundaries. - The loop condition
while (result.size() < rows * cols)ensures that the algorithm continues until all cells in the grid have been visited.
Complexity Analysis
Time Complexity:
- The time complexity of the given algorithm is O(rows _ cols) because in the
whileloop, we traverse the entire matrix once. The loop runsrows _ colstimes in total, where each iteration performs a constant amount of work. - The dominant operations are the
push_backoperation on theresultvector and the conditional checks in theifstatement. These operations are performed within the loop, making the overall time complexity linear with respect to the size of the input matrix. - The Big O classification of O(rows _ cols) is justified because we drop lower-order terms and ignore constants. Therefore, the time complexity can be simplified to O(rows _ cols), where the input size is
rows * cols.
Space Complexity:
- The space complexity of the given algorithm is O(rows _ cols) due to the storage requirements of the
resultvector, which stores the coordinates of the visited cells. In the worst-case scenario, theresultvector will storerows _ colscoordinates. - The
directionsvector and other variables only occupy a constant amount of space and do not impact the overall space complexity. Theresultvector is the primary data structure that affects the space complexity of the algorithm. - Justification of the space complexity is based on the fact that we need to store all the coordinates of the cells in the matrix. This requires O(rows * cols) space to store the
resultvector, making the space complexity linear with respect to the size of the input matrix.
Footnote
This question is rated as Medium difficulty.
Similar Questions:
| Title | URL | Difficulty |
|---|---|---|
| Spiral Matrix | https://leetcode.com/problems/spiral-matrix | Medium |
| Spiral Matrix II | https://leetcode.com/problems/spiral-matrix-ii | Medium |
| Spiral Matrix IV | https://leetcode.com/problems/spiral-matrix-iv | Medium |