Problem 787 Cheapest Flights Within K Stops
Table of Contents
Problem Statement
Link - Problem 787
Question
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1
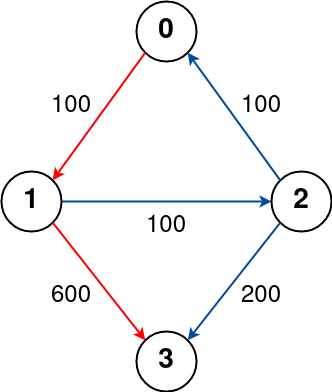
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output: 700
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Example 2
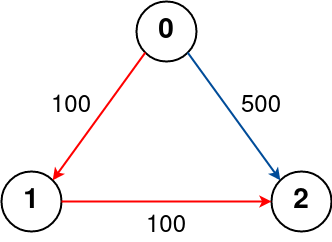
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
Example 3
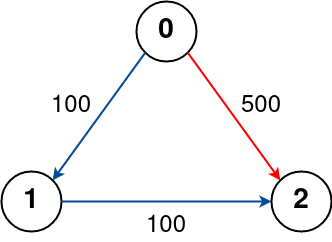
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
Constraints
- `1 <= n <= 100`
- `0 <= flights.length <= (n * (n - 1) / 2)`
- `flights[i].length == 3`
- `0 <= fromi, toi < n`
- `fromi != toi`
- `1 <= pricei <= 10^4`
- There will not be any multiple flights between two cities.
- `0 <= src, dst, k < n`
- `src != dst`
Solution
class Solution {
public:
int dijkstras(int src, vector<vector<pair<int,int>>>&adj, int target, int k,int n){
vector<int>dist(n+1,INT_MAX);
vector<int>stops(n+1,INT_MAX);
dist[src]=0;
stops[src]=0;
priority_queue<vector<int>,vector<vector<int>>,greater<vector<int>>>pq;
pq.push({0,src,0});
while(!pq.empty()){
auto vec = pq.top();
pq.pop();
if(target == vec[1])
return vec[0];
if(vec[2]==k+1)
continue;
for(auto it:adj[vec[1]]){
if(vec[0]+it.second<dist[it.first] || vec[2]+1<stops[it.first]){
dist[it.first] = it.second + vec[0];
stops[it.first] = vec[2]+1;
pq.push({dist[it.first],it.first,stops[it.first]});
}
}
}
return -1;
}
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
vector<vector<pair<int,int>>>adj(n+1);
for(auto it: flights){
adj[it[0]].push_back({it[1],it[2]});
}
return dijkstras(src,adj,dst,k,n);
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| Dijsktras | O(nlogn) | O(n) |
Explanation
1. Intuition
- We can use the Dijkstra algorithm to solve this problem with a slight modification.
- The modification needs to handle the number of stops.
- We can keep track of the number of stops we have made so far.
- If the number of stops exceeds the given number of stops, we can skip that path.
- We can use a priority queue to store the distance, node, and the number of stops.
- If the target node is reached, we can return the distance.
- If the number of stops exceeds the given number of stops, we can skip that path.
- Then for each node adjacent to the current node, we can update the distance and the number of stops.
- Finally, we can return -1 if the target node is not reached.
2. Implementation
- Initialize a function `dijkstras` that takes the source node, adjacency list, target node, number of stops, and the total number of nodes.
- Initialize a vector `dist` to store the distance of each node from the source node.
- Let all the distances be INT_MAX.
- Initialize a vector `stops` to store the number of stops made so far.
- Let all the stops be INT_MAX.
- Set `dist[src]` to 0 and `stops[src]` to 0.
- Initialize a priority queue `pq` to store the `{distance, node, stops}`.
- Push the source node into the priority queue.
- While the priority queue is not empty, pop the top element.
- If the target node is reached, return the distance.
- If the number of stops exceeds the given number of stops, skip that path.
- For each adjacent node of the current node, update the distance and the number of stops.
- Finally, return -1 if the target node is not reached.