Problem 54 Sprial Matrix
Table of Contents
Problem Statement
Link - Problem 54
Question
Given an m x n matrix, return all elements of the matrix in spiral order.
Example 1
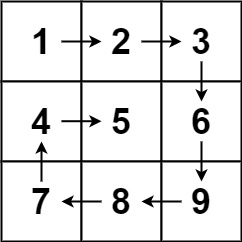
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]
Example 2

Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]
Constraints
- `m == matrix.length`
- `n == matrix[i].length`
- `1 <= m, n <= 10`
- `-100 <= matrix[i][j] <= 100`
Solution
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int rows = matrix.size();
int cols = matrix[0].size();
int row = 0, col = -1;
int direc = 1;
vector<int>ans;
while(rows>0 && cols>0){
for(int i = 0;i<cols;i++){
col+=direc;
ans.push_back(matrix[row][col]);
}
rows--;
for(int i = 0;i<rows;i++){
row+=direc;
ans.push_back(matrix[row][col]);
}
cols--;
direc*=-1;
}
return ans;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| ---------------- | --------------- | ---------------- |
| Matrix Traversal | O(mn) | O(1) |
Explanation
1. Intuition
- To print in spiral order first we should move right, then down, then left and then up.
- We will keep track of the number of rows and columns left to traverse.
- We will keep track of the direction we are moving in.
- We will keep track of the current row and column.
- We will keep adding the elements to the answer vector.
- We will keep updating the rows and columns left to traverse.
- We will keep updating the direction we are moving in.
- The idea is start from the first row and keep moving right till the end of the row.
- Then move down till the end of the column.
- Then move left till the start of the row.
- Then move up till the start of the column.
- Keep doing this till we have traversed all the elements.
2. Implementation
- Initialize the number of `rows = matrix.size()` and `cols = matrix[0].size()`.
- Initialize the current `row = 0` and `col = -1`. They will keep track of the current position.
- The `col` is initialized to `-1` because we will increment it first.
- Initialize the direction `direc = 1`. It will keep track of the direction we are moving in.
- `direc = 1` means we are moving right. `direc = -1` means we are moving left.
- Initialize the answer vector `ans`.
- While we have rows and columns left to traverse.
- Traverse the row from left to right.
- Increment the `col` by `direc`.
- Add the element at the current position to the answer vector.
- Decrement the number of rows left to traverse.
- Traverse the column from top to bottom.
- Increment the `row` by `direc`.
- Add the element at the current position to the answer vector.
- Decrement the number of columns left to traverse.
- Change the direction by multiplying it by `-1`.
- Return the answer vector.
The direction is changed by multiplying it by
-1because we need to change the direction from right to left and from left to right. The direction is changed only after traversing the row and the column. This is because we need to traverse the row and the column in the same direction.