• Posts

Problem 52 N-Queens II

Problem Statement

Link - Problem 52

Question

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example 1:

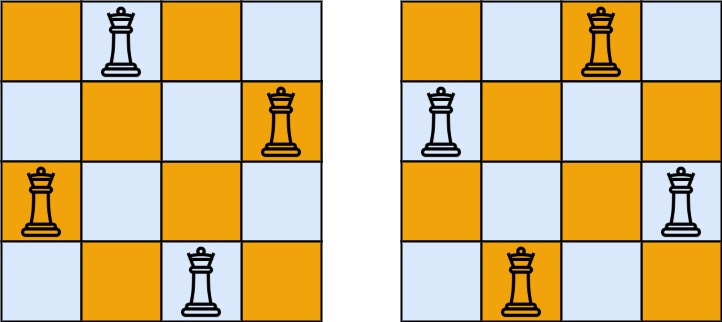
Input: n = 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.

Example 2:

Input: n = 1
Output: 1

Constraints:

• 1 <= n <= 9

Solution

class Solution {
public:
    bool canplacequeen(int row,int col,vector<string>&board){
        for(int i=row-1;i>=0;i--){
            if(board[i][col]=='Q')
                return false;
        }
        for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){
            if(board[i][j]=='Q')
                return false;
        }
        for(int i=row-1,j=col+1;i>=0&&j<board.size();i--,j++){
            if(board[i][j]=='Q')
                return false;
        }
        return true;
    }
    void solvequeen(int row,vector<string> &board,int &count){
        if(row==board.size()){
            count++;
            return;
        }
        for(int col=0;col<board.size();col++){
            if(canplacequeen(row,col,board)){
                board[row][col]='Q';
                solvequeen(row+1,board,count);
                board[row][col]='.';
            }
        }
    }
    int totalNQueens(int n) {
        int count=0;
        vector<string> board(n,string(n,'.'));
        solvequeen(0,board,count);
        return count;
    }
};

Complexity Analysis

| Algorithm    | Time Complexity | Space Complexity |
| ------------ | --------------- | ---------------- |
| Backtracking | O(n!)           | O(n)             |

Explanation

Intial Thoughts

To approach the n-queens puzzle, we should first understand the rules of placing queens on a chessboard, considering that no two queens can attack each other. This involves thinking about how each queen affects the placement of others. We can start by placing queens one by one, ensuring that each placement does not lead to any conflicts. Key points to consider are: think of the problem as placing queens row by row, consider the constraints of a chessboard, think about how each queen placement affects the next, and visualize the problem to understand the queen’s movement patterns.

Intuitive Analysis

Intuitively solving the n-queens puzzle involves breaking it down into manageable steps. This can be achieved by focusing on one row at a time and using a method similar to trial and error, but in a systematic way. Key intuitive strategies include: using backtracking to explore all possible solutions, visualizing the queen’s movement to anticipate conflicts, dividing the problem into smaller sub-problems, considering symmetry to reduce the search space, and using a recursive approach to methodically explore all possible configurations.

1. Intuition

• The n-queens problem is a classic backtracking problem, where we need to place n queens on an n x n chessboard such that no two queens attack each other.
• To solve this problem, we can use a recursive approach, where we try to place a queen in each column of the current row and check if it’s safe to place.
• The key insight is to use a helper function canplacequeen to check if it’s safe to place a queen at a given position.
• We also need to use a recursive function solvequeen to try all possible placements of queens.
• The base case for the recursion is when we have placed all n queens, in which case we increment the count of solutions.
• The time complexity of this solution is O(N!) because in the worst case, we have to try all possible placements of queens.
• The space complexity is O(N) for the recursive call stack and the board.

2. Implementation

• We start by initializing an empty board with n rows and n columns, where n is the input size.
• The canplacequeen function checks if it’s safe to place a queen at a given position by checking the column and the two diagonals.
• The solvequeen function tries to place a queen in each column of the current row and recursively calls itself for the next row.
• We use a count variable to keep track of the number of solutions found.
• The totalNQueens function initializes the board and calls the solvequeen function to start the recursion.
• We use board[row][col] = 'Q' to place a queen at a given position and board[row][col] = '.' to remove a queen.
• The solvequeen function uses a loop to try all possible columns for the current row.

Complexity Analysis

Time Complexity:

• The time complexity of the given solution is O(n!) because in the worst case, the algorithm tries all possible configurations of queens on the board, resulting in n! permutations.
• The dominant operation is the recursive call to solvequeen which is performed n times for each row, leading to a factorial number of operations.
• Using the canplacequeen function to validate each position and the recursive nature of solvequeen justify the O(n!) time complexity due to the exponential growth of operations with the size of the input n.

Space Complexity:

• The space complexity is O(n) because the maximum depth of the recursion tree is n, corresponding to the number of rows on the board.
• The impact of the board data structure, which stores the current configuration of queens, contributes to the space complexity as it requires n strings of length n.
• The recursive call stack, which stores the function calls and local variables, is the primary contributor to the space complexity, justifying the O(n) classification due to its linear growth with the size of the input n.

Footnote

This question is rated as Hard difficulty.

Similar Questions: