Problem 310 Minimum Height Trees
Table of Contents
Problem Statement
Link - Problem 310
Question
A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).
Return a list of all MHTs' root labels. You can return the answer in any order.
The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
Example 1:
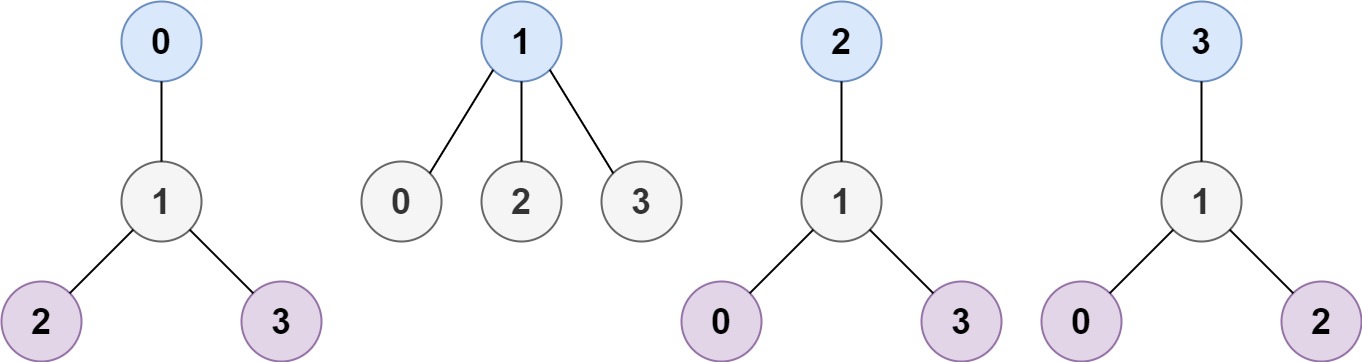
Input: n = 4, edges = [[1,0],[1,2],[1,3]] Output: [1] Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
Example 2:
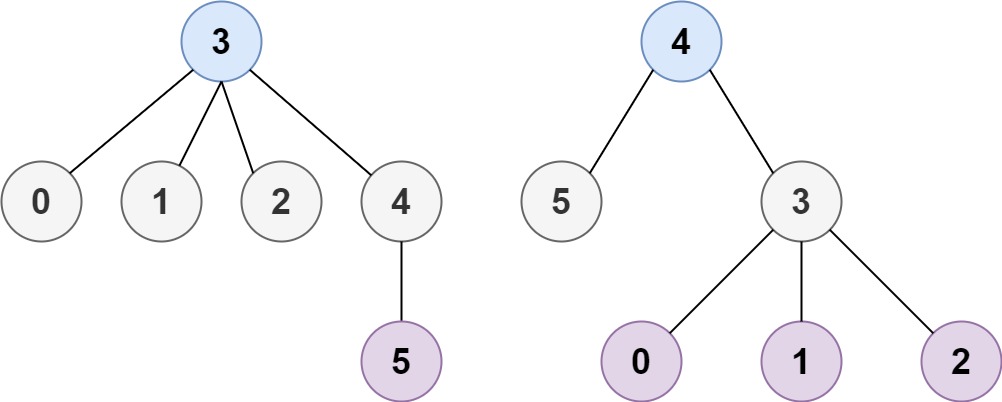
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] Output: [3,4]
Constraints:
1 <= n <= 2 * 104edges.length == n - 10 <= ai, bi < nai != bi- All the pairs
(ai, bi)are distinct. - The given input is guaranteed to be a tree and there will be no repeated edges.
Solution
class Solution {
public:
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
if (n == 1) return {0}; // If there's only one node, it's the root of the tree
std::ios::sync_with_stdio(false);
vector<vector<int>> adj(n);
vector<int> degree(n, 0);
// Step 1: Create an adjacency list and calculate the degree of each node
for (const auto& edge : edges) {
adj[edge[0]].push_back(edge[1]);
adj[edge[1]].push_back(edge[0]);
degree[edge[0]]++;
degree[edge[1]]++;
}
// Step 2: Find the leaves
queue<int> leaves;
for (int i = 0; i < n; ++i) {
if (degree[i] == 1) {
leaves.push(i);
}
}
// Step 3: Perform BFS
while (n > 2) {
int size = leaves.size();
n -= size;
for (int i = 0; i < size; ++i) {
int leaf = leaves.front();
leaves.pop();
for (int neighbor : adj[leaf]) {
degree[neighbor]--;
if (degree[neighbor] == 1) {
leaves.push(neighbor);
}
}
}
}
// Step 4: Return the roots
vector<int> roots;
while (!leaves.empty()) {
roots.push_back(leaves.front());
leaves.pop();
}
return roots;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| -------------------- | --------------- | ---------------- |
| Breadth-first Search | O(n) | O(n) |
Explanation
Intial Thoughts
This is a graph problem that requires finding the minimum height trees by considering all possible roots of the tree. Since it’s a tree, we know it’s connected and has no cycles, so we can start thinking about node degrees and possible paths. The problem can be solved by first identifying the leaves of the tree and then performing a Breadth-First Search (BFS). We also need to think about the cases where there are multiple roots with the same minimum height.
Intuitive Analysis
Start by creating an adjacency list to represent the tree, which allows us to efficiently traverse the graph. Calculate the degree of each node, which is useful for identifying the leaves. Then perform BFS from the leaves, removing them and updating the degrees until only the roots are left. Use a queue to keep track of the nodes to be removed and consider multiple roots as the final answer if they have the same minimum height. Finally, analyze the logic and apply it to edge cases to ensure correctness.
1. Intuition
- The problem asks to find the roots of the minimum height trees in a given tree.
- To solve this problem, we can use a topological sorting approach.
- We start by finding the leaves of the tree, which are the nodes with degree 1.
- Then, we iteratively remove the leaves from the tree until we are left with 1 or 2 nodes.
- These remaining nodes are the roots of the minimum height trees.
- This approach works because the height of the tree is minimized when the root is chosen to be the node with the maximum degree.
- By removing the leaves iteratively, we ensure that the height of the tree is minimized.
2. Implementation
- We create an adjacency list
adjto represent the tree, whereadj[i]is the list of neighbors of nodei. - We also create a degree array
degreeto keep track of the degree of each node. - We initialize the degree array by iterating over the edges and incrementing the degree of each node by 1 for each edge.
- We find the leaves of the tree by iterating over the degree array and adding the nodes with degree 1 to a queue
leaves. - We perform a BFS traversal of the tree by iteratively removing the leaves from the queue and updating the degree array.
- We repeat this process until we are left with 1 or 2 nodes in the queue, which are the roots of the minimum height trees.
- We return the roots of the minimum height trees by popping the nodes from the queue and adding them to the result vector.
Complexity Analysis
Time Complexity:
- The time complexity is dominated by the creation of the adjacency list and the BFS traversal. The
forloop in Step 1 iterates over all edges, resulting in O(|E|) complexity, where |E| is the number of edges. Since |E| is at most n-1 in a tree, this reduces to O(n). - The
whileloop in Step 3 iterates until n > 2, and in each iteration, it processes all leaves. The total number of leaves processed across all iterations equals the total number of nodes, resulting in O(n) complexity. - The overall time complexity is O(n) due to these dominant operations.
Space Complexity:
- The space complexity is dominated by the adjacency list and the queue used in BFS. The adjacency list stores all edges, resulting in O(n + |E|) space complexity, where n is the number of nodes and |E| is the number of edges.
- The queue stores at most n leaves at any given time, resulting in O(n) space complexity.
- The overall space complexity is O(n) because the adjacency list’s space complexity reduces to O(n) in a tree, where |E| is at most n-1.
Footnote
This question is rated as Medium difficulty.
Hints
How many MHTs can a graph have at most?
Similar Questions:
| Title | URL | Difficulty |
|---|---|---|
| Course Schedule | https://leetcode.com/problems/course-schedule | Medium |
| Course Schedule II | https://leetcode.com/problems/course-schedule-ii | Medium |
| Collect Coins in a Tree | https://leetcode.com/problems/collect-coins-in-a-tree | Hard |
| Count Pairs of Connectable Servers in a Weighted Tree Network | https://leetcode.com/problems/count-pairs-of-connectable-servers-in-a-weighted-tree-network | Medium |
| Find Minimum Diameter After Merging Two Trees | https://leetcode.com/problems/find-minimum-diameter-after-merging-two-trees | Hard |