• Posts

Problem 2684 Maximum Number of Moves in a Grid

Problem Statement

Link - Problem 2684

Question

You are given a 0-indexed m x n matrix grid consisting of positive integers.

You can start at any cell in the first column of the matrix, and traverse the grid in the following way:

• From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.

Return the maximum number of moves that you can perform.

Example 1:

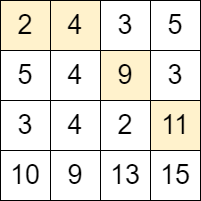
Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
Output: 3
Explanation: We can start at the cell (0, 0) and make the following moves:
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
It can be shown that it is the maximum number of moves that can be made.

Example 2:

Input: grid = [[3,2,4],[2,1,9],[1,1,7]]
Output: 0
Explanation: Starting from any cell in the first column we cannot perform any moves.

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 106

Solution

class Solution {
public:
    int maxMoves(vector<vector<int>>& grid) {
        int rows = grid.size();
        int cols = grid[0].size();
        int answer = 0;

        vector<vector<int>> dp(rows, vector<int>(cols, 0));

        for (int col = cols - 1; col >= 0; col--) {
            for (int row = 0; row < rows; row++) {
                int diag_up = 0, right = 0, diag_down = 0;

                if (row - 1 >= 0 && col + 1 < cols && grid[row - 1][col + 1] > grid[row][col]) {
                    diag_up = 1 + dp[row - 1][col + 1];
                }

                if (col + 1 < cols && grid[row][col + 1] > grid[row][col]) {
                    right = 1 + dp[row][col + 1];
                }

                if (row + 1 < rows && col + 1 < cols && grid[row + 1][col + 1] > grid[row][col]) {
                    diag_down = 1 + dp[row + 1][col + 1];
                }

                dp[row][col] = max(diag_up, max(right, diag_down));

                if (col == 0) {
                    answer = max(answer, dp[row][0]);
                }
            }
        }

        return answer;
    }
};

Complexity Analysis

| Algorithm           | Time Complexity | Space Complexity |
| ------------------- | --------------- | ---------------- |
| Dynamic Programming | O(nm)           | O(nm)            |

Explanation

Intial Thoughts

To start, think of the grid as a maze where each cell has a specific value. Consider that you can only move right, and in order to do so, you must find a cell with a higher value than the current one. Think about how you can use this constraint to limit the possible moves. Consider starting from the last column and working your way back to the first, keeping track of the maximum number of moves you can make from each cell. Use this information to narrow down the possible paths and find the longest one.

Intuitive Analysis

Imagine each cell in the grid as a mountain with a certain height, where you can only climb to a higher mountain. From each mountain, you have three options to move to the next column: up and to the right, directly to the right, or down and to the right. You can only take a step if the next mountain is higher, so you need to keep track of the maximum height you can reach from each mountain. By working backwards from the last column, you can build a map of the maximum heights, which will help you find the longest path from the first column to the last.

1. Intuition

• The problem can be approached using dynamic programming, where we build up a solution by computing the maximum number of moves for each cell in the grid.
• We start from the last column and move backwards to the first column, ensuring that we have the maximum number of moves for each cell in the current column before moving to the previous column.
• The key insight is to consider the three possible moves from each cell: diagonally up, right, and diagonally down, and choose the one that results in the maximum number of moves.
• We need to ensure that the value of the cell we move to is strictly bigger than the value of the current cell, which is a crucial constraint in the problem.
• By using dynamic programming, we avoid recomputing the maximum number of moves for each cell, which reduces the time complexity of the solution.
• The solution works by iteratively updating the dp array, where dp[row][col] represents the maximum number of moves that can be performed starting from the cell at (row, col).
• The algorithmic choice of using dynamic programming allows us to solve the problem efficiently, with a time complexity of O(m*n), where m and n are the number of rows and columns in the grid, respectively.
• The space complexity is also O(m*n), as we need to store the dp array, which has the same size as the input grid.

2. Implementation

• We initialize the dp array with zeros, where dp[row][col] will store the maximum number of moves that can be performed starting from the cell at (row, col).
• We iterate over the columns in reverse order, starting from the last column and moving backwards to the first column, using the loop for (int col = cols - 1; col >= 0; col--).
• For each cell in the current column, we compute the maximum number of moves by considering the three possible moves: diagonally up, right, and diagonally down, using the variables diag_up, right, and diag_down.
• We update the dp array using the maximum number of moves computed for each cell, using the line dp[row][col] = max(diag_up, max(right, diag_down)).
• We keep track of the maximum number of moves that can be performed starting from any cell in the first column, using the variable answer and the line answer = max(answer, dp[row][0]).
• Finally, we return the maximum number of moves that can be performed, which is stored in the answer variable.
• The dp array is used to store the intermediate results, which allows us to avoid recomputing the maximum number of moves for each cell, using the line int diag_up = 0, right = 0, diag_down = 0;.

Complexity Analysis

Time Complexity:

• The algorithm has two nested loops, one iterating over each column (for (int col = cols - 1; col >= 0; col--)) and another over each row (for (int row = 0; row < rows; row--)), resulting in a total of n*m iterations, where n is the number of rows and m is the number of columns.
• The dominant operations within the loop are constant time comparisons and assignments, such as diag_up = 1 + dp[row - 1][col + 1];, which do not affect the overall time complexity.
• Therefore, the time complexity is O(n*m) because the algorithm visits each cell in the grid once, and the number of operations is directly proportional to the size of the input grid.

Space Complexity:

• The algorithm uses a 2D vector dp of size n*m to store the dynamic programming state, where n is the number of rows and m is the number of columns.
• The space complexity is dominated by the dp vector, which requires O(n*m) space to store the intermediate results for each cell in the grid.
• Therefore, the space complexity is O(n*m) because the amount of memory used grows linearly with the size of the input grid.

Footnote

This question is rated as Medium difficulty.

Hints

Consider using dynamic programming to find the maximum number of moves that can be made from each cell.

The final answer will be the maximum value in cells of the first column.