The Indian Engineer

Problem 2463 Minimum Total Distance Traveled

Posted on 8 mins

Array Dynamic-Programming Sorting

Table of Contents

Problem Statement

Link - Problem 2463

Question

There are some robots and factories on the X-axis. You are given an integer array robot where robot[i] is the position of the ith robot. You are also given a 2D integer array factory where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.

The positions of each robot are unique. The positions of each factory are also unique. Note that a robot can be in the same position as a factory initially.

All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.

At any moment, you can set the initial direction of moving for some robot. Your target is to minimize the total distance traveled by all the robots.

Return the minimum total distance traveled by all the robots. The test cases are generated such that all the robots can be repaired.

Note that

Example 1:

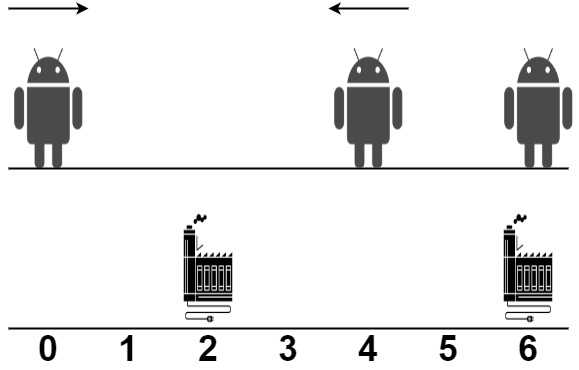
Input: robot = [0,4,6], factory = [[2,2],[6,2]]
Output: 4
Explanation: As shown in the figure:
- The first robot at position 0 moves in the positive direction. It will be repaired at the first factory.
- The second robot at position 4 moves in the negative direction. It will be repaired at the first factory.
- The third robot at position 6 will be repaired at the second factory. It does not need to move.
The limit of the first factory is 2, and it fixed 2 robots.
The limit of the second factory is 2, and it fixed 1 robot.
The total distance is |2 - 0| + |2 - 4| + |6 - 6| = 4. It can be shown that we cannot achieve a better total distance than 4.

Example 2:

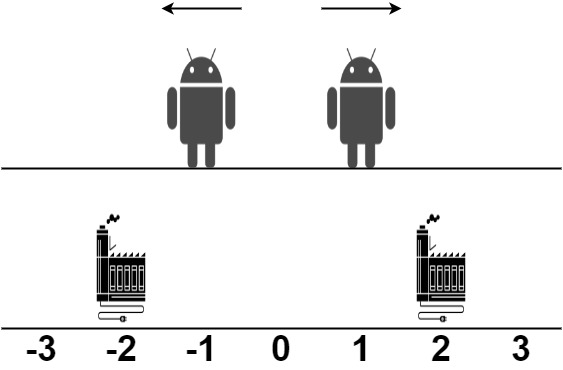
Input: robot = [1,-1], factory = [[-2,1],[2,1]]
Output: 2
Explanation: As shown in the figure:
- The first robot at position 1 moves in the positive direction. It will be repaired at the second factory.
- The second robot at position -1 moves in the negative direction. It will be repaired at the first factory.
The limit of the first factory is 1, and it fixed 1 robot.
The limit of the second factory is 1, and it fixed 1 robot.
The total distance is |2 - 1| + |(-2) - (-1)| = 2. It can be shown that we cannot achieve a better total distance than 2.

Constraints:

Solution 

class Solution {
public:
    long long minimumTotalDistance(vector<int>& robot, vector<vector<int>>& factory) {
        sort(robot.begin(), robot.end());
        sort(factory.begin(), factory.end());

        vector<int> factoryPositions;
        for (auto& f : factory)
            for (int i = 0; i < f[1]; i++)
                factoryPositions.push_back(f[0]);

        int robotCount = robot.size(), factoryCount = factoryPositions.size();
        vector<vector<long long>> memo(robotCount, vector<long long>(factoryCount, -1));

        return calculateMinDistance(0, 0, robot, factoryPositions, memo);
    }

    long long calculateMinDistance(int robotIdx, int factoryIdx, vector<int>& robot, vector<int>& factoryPositions, vector<vector<long long>>& memo) {
        if (robotIdx == robot.size())
            return 0;

        if (factoryIdx == factoryPositions.size())
            return 1e12;

        if (memo[robotIdx][factoryIdx] != -1)
            return memo[robotIdx][factoryIdx];

        long long assign = abs(robot[robotIdx] - factoryPositions[factoryIdx]) + calculateMinDistance(robotIdx + 1, factoryIdx + 1, robot, factoryPositions, memo);

        long long skip = calculateMinDistance(robotIdx, factoryIdx + 1, robot, factoryPositions, memo);

        return memo[robotIdx][factoryIdx] = min(assign, skip);
    }
};

Complexity Analysis 

| Algorithm                            | Time Complexity | Space Complexity |
| ------------------------------------ | --------------- | ---------------- |
| Dynamic Programming with Memoization | O(n m)          | O(nm)            |

Explanation

Intial Thoughts

To approach this problem, consider the positions of the robots and factories on the X-axis. Think of the robots as needing to move to the nearest available factory that has not reached its repair limit. The goal is to minimize the total distance traveled. Key points include: sorting the robots and factories by position to efficiently process them, using dynamic programming to store and reuse the results of subproblems, and considering the trade-offs between assigning a robot to the current factory versus skipping it and moving on to the next one.

Intuitive Analysis

Intuitively, the problem can be solved by visualizing the movement of the robots as a series of decisions about which factory to move towards, given the constraints on the number of robots each factory can repair. The analysis involves breaking down the problem into smaller subproblems, such as deciding whether to assign a robot to the current factory or to skip it, and using the results of these subproblems to inform the overall solution. Key points include: the importance of sorting the input to enable efficient processing, the use of memoization to avoid redundant calculations, and the need to balance the competing demands of minimizing distance traveled with the constraints on factory capacity.

1. Intuition

2. Implementation

Complexity Analysis

Time Complexity:

Space Complexity:

Footnote

This question is rated as Hard difficulty.

Hints

Sort robots and factories by their positions.

After sorting, notice that each factory should repair some subsegment of robots.

Find the minimum total distance to repair first i robots with first j factories.

Similar Questions:

Title URL Difficulty
Capacity To Ship Packages Within D Days https://leetcode.com/problems/capacity-to-ship-packages-within-d-days Medium
Number of Ways to Earn Points https://leetcode.com/problems/number-of-ways-to-earn-points Hard