Problem 2392 Build a Matrix With Conditions
Table of Contents
Problem Statement
Link - Problem 2392
Question
You are given a positive integer k. You are also given:
- a 2D integer array
rowConditionsof sizenwhererowConditions[i] = [abovei, belowi], and - a 2D integer array
colConditionsof sizemwherecolConditions[i] = [lefti, righti].
The two arrays contain integers from 1 to k.
You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.
The matrix should also satisfy the following conditions:
- The number
aboveishould appear in a row that is strictly above the row at which the numberbelowiappears for allifrom0ton - 1. - The number
leftishould appear in a column that is strictly left of the column at which the numberrightiappears for allifrom0tom - 1.
Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.
Example 1:
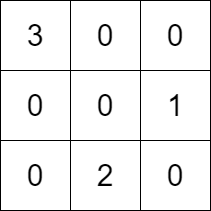
Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]] Output: [[3,0,0],[0,0,1],[0,2,0]] Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions. The row conditions are the following: - Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix. - Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix. The column conditions are the following: - Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix. - Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix. Note that there may be multiple correct answers.
Example 2:
Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]] Output: [] Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied. No matrix can satisfy all the conditions, so we return the empty matrix.
Constraints:
2 <= k <= 4001 <= rowConditions.length, colConditions.length <= 104rowConditions[i].length == colConditions[i].length == 21 <= abovei, belowi, lefti, righti <= kabovei != belowilefti != righti
Solution
class Solution {
public:
vector<int> topologicalOrder(int k, vector<vector<int>>&conditions){
vector<int>deg(k+1,0);
vector<vector<int>>adj(k+1);
for(auto& edge:conditions){
adj[edge[0]].push_back(edge[1]);
deg[edge[1]]++;
}
queue<int>q;
for(int i=1; i<=k; i++){
if(deg[i]==0)
q.push(i);
}
int count = 0;
vector<int>order;
while(!q.empty()){
int i = q.front();
q.pop();
order.push_back(i);
count++;
for(int j:adj[i]){
deg[j]--;
if(deg[j]==0)
q.push(j);
}
}
if(count!=k)
return {};
return order;
}
vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {
auto rowOrder = topologicalOrder(k,rowConditions);
auto colOrder = topologicalOrder(k,colConditions);
//for(auto it:rowOrder)
//cout<<it<<" ";
if(rowOrder.empty() || colOrder.empty())
return {};
vector<vector<int>>ans(k,vector<int>(k));
vector<int>posX(k+1),posY(k+1);
for(int i=0;i<k;i++){
posX[rowOrder[i]] = i;
posY[colOrder[i]] = i;
}
for(int i=1;i<=k;i++){
ans[posX[i]][posY[i]] = i;
}
return ans;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| -------------------------- | --------------- | ---------------- |
| Kahn's Topological Sorting | O(k + c) | O(k + c) |
Explanation
Intial Thoughts
To solve this problem, we need to think about how to place the numbers 1 to k in a k x k matrix in a way that satisfies the given row and column conditions. We can start by considering the row conditions, which specify that a certain number should be placed above another number. Then, we can think about the column conditions, which specify that a certain number should be placed to the left of another number. We should look for a way to find a valid ordering of the numbers that satisfies both the row and column conditions.
Intuitive Analysis
One way to intuitively solve this problem is to use the concept of topological sorting. We can create a graph based on the row and column conditions and then find a valid ordering of the numbers using topological sorting. If there is a cycle in the graph, it means that there is no valid ordering and we should return an empty matrix. Otherwise, we can use the ordering to place the numbers in the matrix. We should also consider how to handle the cases where there are multiple valid orderings and how to choose one that satisfies the conditions.
1. Intuition
- The problem requires building a k x k matrix with numbers from 1 to k, satisfying row and column conditions.
- To solve this, we can use topological sorting to order the numbers based on the given conditions.
- We need to ensure that the number above_i appears in a row strictly above the row at which the number below_i appears.
- Similarly, the number left_i should appear in a column strictly left of the column at which the number right_i appears.
- If there’s a cycle in the conditions, it’s impossible to satisfy all conditions, so we return an empty matrix.
- The topologicalOrder function helps us find a valid order for the numbers, and if no such order exists, it returns an empty vector.
- We use the topologicalOrder function for both row and column conditions to get the valid orders.
- Then, we use these orders to fill in the matrix, ensuring that each number appears exactly once.
2. Implementation
- We define a function
topologicalOrderthat takes k and conditions as input and returns a vector of numbers in a valid order. - In the
topologicalOrderfunction, we use a queueqto store numbers with no incoming edges and a vectororderto store the result. - We iterate over the conditions to build the adjacency list
adjand calculate the in-degreedegof each number. - We then iterate over the numbers from 1 to k, and if a number has no incoming edges, we add it to the queue
q. - We use a while loop to process the numbers in the queue, adding them to the
ordervector and updating the in-degrees of their neighbors. - If the length of the
ordervector is not equal to k, it means there’s a cycle, so we return an empty vector. - In the
buildMatrixfunction, we calltopologicalOrderfor both row and column conditions to get the valid orders. - We then use these orders to fill in the matrix, ensuring that each number appears exactly once, using
posXandposYvectors to store the positions of the numbers.
Complexity Analysis
Time Complexity:
- The time complexity is driven by the
forloops that iterate through theconditionsand the queue operations in thetopologicalOrdermethod. The outer loop inbuildMatrixalso contributes to the time complexity. - The dominant operations are the construction of the adjacency list
adjand the queue operations. These operations depend on the number of conditionscand the number of nodesk. Hence, the time complexity is O(k + c). - The justification of the Big O classification comes from the fact that the algorithm performs a constant amount of work for each node and each condition, resulting in a linear time complexity.
Space Complexity:
- The memory usage is mainly due to the storage of the adjacency list
adj, the degree arraydeg, and the queueq. The space required also depends on the size of the output matrixans. - The data structures used, such as vectors and queues, have a direct impact on the space complexity. The size of these data structures grows linearly with the number of nodes
kand conditionsc. - The justification of the space complexity comes from the fact that the algorithm uses a constant amount of space for each node and each condition, resulting in a space complexity of O(k + c).
Footnote
This question is rated as Hard difficulty.
Hints
Can you think of the problem in terms of graphs?
What algorithm allows you to find the order of nodes in a graph?
Similar Questions:
| Title | URL | Difficulty |
|---|---|---|
| Course Schedule | https://leetcode.com/problems/course-schedule | Medium |
| Course Schedule II | https://leetcode.com/problems/course-schedule-ii | Medium |
| Find Eventual Safe States | https://leetcode.com/problems/find-eventual-safe-states | Medium |
| Loud and Rich | https://leetcode.com/problems/loud-and-rich | Medium |