Problem 2045 Second Minimum Time to Reach Destination
Table of Contents
Problem Statement
Link - Problem 2045
Question
A city is represented as a bi-directional connected graph with n vertices where each vertex is labeled from 1 to n (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself. The time taken to traverse any edge is time minutes.
Each vertex has a traffic signal which changes its color from green to red and vice versa every change minutes. All signals change at the same time. You can enter a vertex at any time, but can leave a vertex only when the signal is green. You cannot wait at a vertex if the signal is green.
The second minimum value is defined as the smallest value strictly larger than the minimum value.
- For example the second minimum value of
[2, 3, 4]is3, and the second minimum value of[2, 2, 4]is4.
Given n, edges, time, and change, return the second minimum time it will take to go from vertex 1 to vertex n.
Notes:
- You can go through any vertex any number of times, including
1andn. - You can assume that when the journey starts, all signals have just turned green.
Example 1:
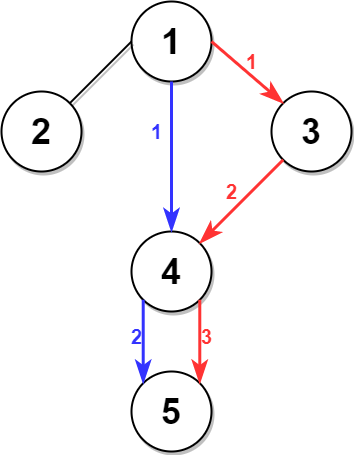
Input: n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5 Output: 13 Explanation: The figure on the left shows the given graph. The blue path in the figure on the right is the minimum time path. The time taken is: - Start at 1, time elapsed=0 - 1 -> 4: 3 minutes, time elapsed=3 - 4 -> 5: 3 minutes, time elapsed=6 Hence the minimum time needed is 6 minutes.The red path shows the path to get the second minimum time.
- Start at 1, time elapsed=0
- 1 -> 3: 3 minutes, time elapsed=3
- 3 -> 4: 3 minutes, time elapsed=6
- Wait at 4 for 4 minutes, time elapsed=10
- 4 -> 5: 3 minutes, time elapsed=13 Hence the second minimum time is 13 minutes.
Example 2:

Input: n = 2, edges = [[1,2]], time = 3, change = 2 Output: 11 Explanation: The minimum time path is 1 -> 2 with time = 3 minutes. The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes.
Constraints:
2 <= n <= 104n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)edges[i].length == 21 <= ui, vi <= nui != vi- There are no duplicate edges.
- Each vertex can be reached directly or indirectly from every other vertex.
1 <= time, change <= 103
Solution
class Solution {
public:
int stepsTime(int steps, int time, int change) {
int res = 0;
while (--steps) {
res += time;
if ((res / change) % 2)
res = (res / change + 1) * change;
}
return res + time;
}
int secondMinimum(int n, vector<vector<int>>& edges, int time, int change) {
vector<vector<int>> adj(n + 1);
vector<int> minSteps(n + 1, 10001);
for (auto &e : edges) {
adj[e[0]].push_back(e[1]);
adj[e[1]].push_back(e[0]);
}
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, 1});
while(!pq.empty() && pq.top().first <= minSteps[n] + 1) {
auto [step, i] = pq.top();
while (!pq.empty() && pq.top().first == step && pq.top().second == i)
pq.pop();
minSteps[i] = min(minSteps[i], step);
if (i == n && step > minSteps[n])
return stepsTime(step, time, change);
if (step <= minSteps[i] + 1)
for (int j : adj[i])
pq.push({step + 1, j});
}
return stepsTime(minSteps[n] + 2, time, change);
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| -------------------- | --------------- | ---------------- |
| Dijkstra's algorithm | O(n + m log n) | O(n + m) |
Explanation
Intial Thoughts
The problem involves finding the second minimum time to traverse a bi-directional connected graph from vertex 1 to vertex n. Initial thoughts include understanding the graph structure, the traffic signal rules, and how to calculate the time taken to traverse each edge. Key considerations are the time taken to traverse an edge, the change interval of the traffic signal, and the constraint of not waiting at a vertex if the signal is green.
Intuitive Analysis
To intuitively solve this problem, we need to think about the possible paths from vertex 1 to vertex n and how the traffic signal affects the time taken for each path. We can imagine the graph as a network of roads with traffic lights, and we need to find the two shortest paths from the starting point to the destination, considering the traffic light rules. The second minimum time will be the time taken for the second shortest path, taking into account any waiting time at the traffic lights.
1. Intuition
- The problem can be approached by using a priority queue to keep track of the minimum steps required to reach each vertex.
- We need to consider the time taken to traverse each edge and the time taken to wait at each vertex for the signal to turn green.
- The key insight is to use a
stepsTimefunction to calculate the time taken to traverse a certain number of steps, taking into account the time taken to wait at each vertex. - We also need to keep track of the minimum steps required to reach each vertex, and update this information as we traverse the graph.
- The solution works by using a priority queue to efficiently explore the graph and keep track of the minimum steps required to reach each vertex.
- The algorithmic choice of using a priority queue allows us to efficiently explore the graph and find the second minimum time required to reach the destination vertex.
- The time complexity of the solution is O(n + m log n), where n is the number of vertices and m is the number of edges.
- The space complexity of the solution is O(n + m), where n is the number of vertices and m is the number of edges.
2. Implementation
- The
stepsTimefunction is implemented asint stepsTime(int steps, int time, int change) { ... }to calculate the time taken to traverse a certain number of steps. - The
secondMinimumfunction is implemented asint secondMinimum(int n, vector<vector<int>>& edges, int time, int change) { ... }to find the second minimum time required to reach the destination vertex. - The
adjvector is used to represent the adjacency list of the graph, whereadj[i]contains the vertices that are directly connected to vertexi. - The
minStepsvector is used to keep track of the minimum steps required to reach each vertex, whereminSteps[i]contains the minimum steps required to reach vertexi. - The
pqpriority queue is used to efficiently explore the graph and keep track of the minimum steps required to reach each vertex. - The
whileloop is used to iterate over the vertices in the priority queue and update theminStepsvector accordingly. - The
ifstatement is used to check if the current vertex is the destination vertex, and if so, return the second minimum time required to reach it. - The
forloop is used to iterate over the adjacent vertices of the current vertex and update theminStepsvector accordingly.
Complexity Analysis
Time Complexity:
- The
whileloop and theforloop within the Dijkstra’s algorithm implementation contribute to the time complexity, where thewhileloop runs in O(m log n) due to the priority queue operations and theforloop runs in O(n + m) for building the adjacency list. - The dominant operation is the
pq.pushandpq.popoperations within thewhileloop, which take O(log n) time, resulting in a total time complexity of O(n + m log n). - The time complexity is justified as O(n + m log n) because the algorithm visits each node and edge once, and the priority queue operations add a logarithmic factor.
Space Complexity:
- The space complexity is mainly due to the storage of the adjacency list
adjand the priority queuepq, which require O(n + m) space. - The
minStepsarray and other variables require additional O(n) space, but this is dominated by the space required for the adjacency list and priority queue. - The overall space complexity is O(n + m) because the algorithm needs to store the graph structure and the minimum distance information for each node.
Footnote
This question is rated as Hard difficulty.
Hints
How much is change actually necessary while calculating the required path?
How many extra edges do we need to add to the shortest path?
Similar Questions:
| Title | URL | Difficulty |
|---|---|---|
| Network Delay Time | https://leetcode.com/problems/network-delay-time | Medium |
| Find the City With the Smallest Number of Neighbors at a Threshold Distance | https://leetcode.com/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance | Medium |
| Number of Ways to Arrive at Destination | https://leetcode.com/problems/number-of-ways-to-arrive-at-destination | Medium |