Problem 1937 Maximum Number of Points with Cost
Table of Contents
Problem Statement
Link - Problem 1937
Question
You are given an m x n integer matrix points (0-indexed). Starting with 0 points, you want to maximize the number of points you can get from the matrix.
To gain points, you must pick one cell in each row. Picking the cell at coordinates (r, c) will add points[r][c] to your score.
However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows r and r + 1 (where 0 <= r < m - 1), picking cells at coordinates (r, c1) and (r + 1, c2) will subtract abs(c1 - c2) from your score.
Return the maximum number of points you can achieve.
abs(x) is defined as:
xforx >= 0.-xforx < 0.
Example 1:
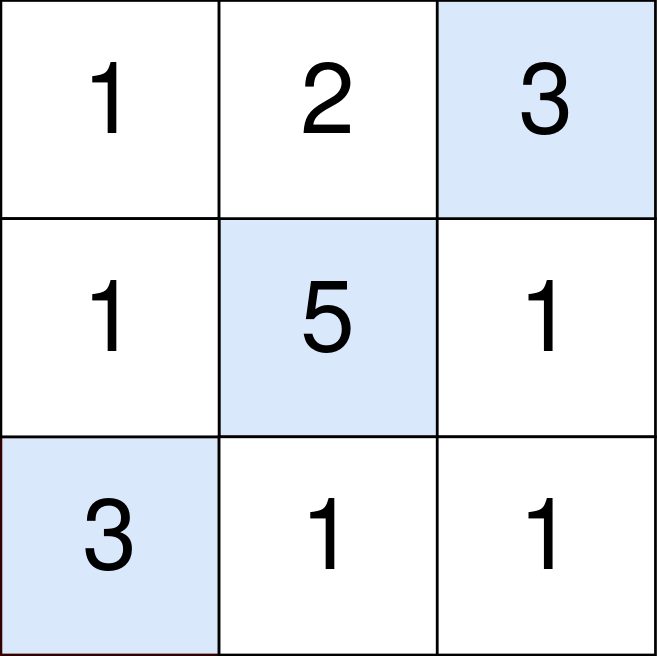
Input: points = [[1,2,3],[1,5,1],[3,1,1]] Output: 9 Explanation: The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0). You add 3 + 5 + 3 = 11 to your score. However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score. Your final score is 11 - 2 = 9.
Example 2:
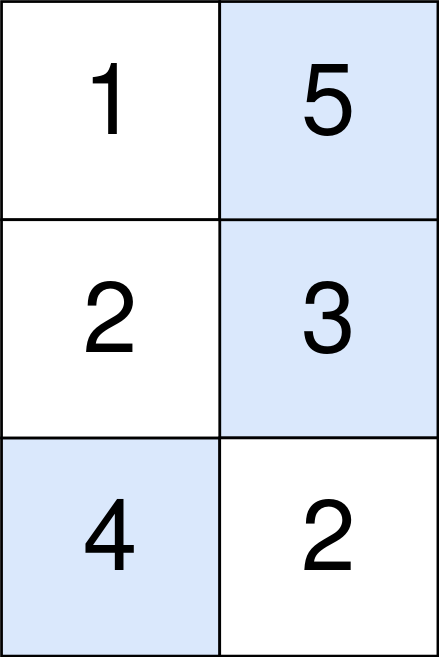
Input: points = [[1,5],[2,3],[4,2]] Output: 11 Explanation: The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0). You add 5 + 3 + 4 = 12 to your score. However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score. Your final score is 12 - 1 = 11.
Constraints:
m == points.lengthn == points[r].length1 <= m, n <= 1051 <= m * n <= 1050 <= points[r][c] <= 105
Solution
class Solution {
public:
long long maxPoints(vector<vector<int>>& points) {
vector<vector<long long>> dp(points.size(), vector<long long>(points[0].size(), -1));
for (int i = 0; i < points[0].size(); ++i) {
dp[0][i] = points[0][i];
}
for (int i = 1; i < points.size(); ++i) {
vector<long long> left_dp(points[i].size(), -1);
vector<long long> right_dp(points[i].size(), -1);
left_dp[0] = dp[i - 1][0];
for (int k = 1; k < points[i].size(); ++k) {
left_dp[k] = max(left_dp[k - 1], dp[i - 1][k] + k);
}
right_dp.back() = dp[i - 1].back() - points[i].size() + 1;
for (int k = points[i].size() - 2; k >= 0; --k) {
right_dp[k] = max(right_dp[k + 1], dp[i - 1][k] - k);
}
for (int j = 0; j < points[i].size(); ++j) {
dp[i][j] = max(left_dp[j] - j, right_dp[j] + j) + points[i][j];
}
}
long long max_ans = -1;
for (const auto v : dp.back()) {
max_ans = max(max_ans, v);
}
return max_ans;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| ------------------- | --------------- | ---------------- |
| Dynamic Programming | O(nm) | O(nm) |
Explanation
Intial Thoughts
To approach this problem, first consider the constraints and the goal. We need to maximize the points gained from the matrix by picking one cell in each row. The points gained from each cell are added to the score, but we lose points if the picked cells are too far apart in adjacent rows. We should start by analyzing how the points are distributed in the matrix and think about strategies to minimize the loss of points due to distance. The problem can be broken down into smaller sub-problems, and we should look for patterns or relationships between rows to find an optimal solution.
Intuitive Analysis
Intuitively, we can think of this problem as trying to find a path through the matrix that maximizes the points gained. We should consider the trade-off between gaining points from a cell and losing points due to its distance from the previous cell. A greedy approach might not work because we need to consider the long-term effects of our choices. Instead, we can use dynamic programming to build up a solution by considering the optimal choices for each row based on the previous row. By analyzing the problem in this way, we can develop a strategy to find the maximum points that can be achieved.
1. Intuition
- The problem can be approached using dynamic programming, where we build up a solution by considering each row of the matrix one by one.
- We need to keep track of the maximum points that can be achieved for each cell in the current row, considering the points achieved in the previous row.
- The key insight is to realize that the maximum points for a cell in the current row depends on the maximum points achieved in the previous row, and the difference in column indices between the two cells.
- We can use two arrays,
left_dpandright_dp, to keep track of the maximum points that can be achieved by moving to the left or right from the previous row. - The
left_dparray is used to keep track of the maximum points that can be achieved by moving to the left, and theright_dparray is used to keep track of the maximum points that can be achieved by moving to the right. - The final solution is the maximum points that can be achieved in the last row, which is stored in the
dparray. - The time complexity of the solution is O(m*n), where m is the number of rows and n is the number of columns in the matrix.
- The space complexity of the solution is also O(m*n), as we need to store the
dparray.
2. Implementation
- We initialize the
dparray with -1, and then fill it up row by row using theleft_dpandright_dparrays. - The
left_dparray is filled up from left to right, using themaxfunction to keep track of the maximum points that can be achieved by moving to the left. - The
right_dparray is filled up from right to left, using themaxfunction to keep track of the maximum points that can be achieved by moving to the right. - We then fill up the
dparray using theleft_dpandright_dparrays, by taking the maximum of the two and adding the points for the current cell. - The final solution is the maximum points that can be achieved in the last row, which is stored in the
dparray. - We use the
maxfunction to keep track of the maximum points that can be achieved, and theabsfunction to calculate the difference in column indices between two cells. - The
pointsarray is used to store the points for each cell in the matrix, and thedparray is used to store the maximum points that can be achieved for each cell. - The solution is implemented using a bottom-up dynamic programming approach, where we build up the solution by considering each row of the matrix one by one.
Complexity Analysis
Time Complexity:
- The algorithm has two nested loops, where the outer loop
for (int i = 1; i < points.size(); ++i)runsntimes and the inner loopfor (int k = 1; k < points[i].size(); ++k)andfor (int k = points[i].size() - 2; k >= 0; --k)each runmtimes. This results in a time complexity of O(nm) due to the nested iterations over thepointsvector. - The dominant operations are the
maxfunction calls within the inner loops, which are used to calculate the maximum points for each row. These operations do not depend on the size of the input but are performed for each element in thepointsvector. - The Big O classification of O(nm) is justified because the algorithm’s running time grows linearly with the product of the number of rows
nand the number of columnsmin thepointsvector.
Space Complexity:
- The algorithm uses a 2D vector
dpwith dimensionsnbymto store the maximum points for each cell, resulting in a space complexity of O(nm). - The additional space used by the
left_dpandright_dpvectors does not change the overall space complexity, as their sizes are also proportional tom. - The space complexity is justified because the algorithm requires a data structure that scales with the size of the input
pointsvector, and thedpvector is the primary data structure used to store the intermediate results.
Footnote
This question is rated as Medium difficulty.
Hints
Try using dynamic programming.
dp[i][j] is the maximum number of points you can have if points[i][j] is the most recent cell you picked.
Similar Questions:
| Title | URL | Difficulty |
|---|---|---|
| Minimum Path Sum | https://leetcode.com/problems/minimum-path-sum | Medium |
| Minimize the Difference Between Target and Chosen Elements | https://leetcode.com/problems/minimize-the-difference-between-target-and-chosen-elements | Medium |