The Indian Engineer

Problem 138 Copy List with Random Pointer

Posted on 7 mins

Hash-Table Linked-List

Table of Contents

Problem Statement

Link - Problem 138

Question

A linked list of length n is given such that each node contains an additional random pointer, which could point to any node in the list, or null.

Construct a deep copy of the list. The deep copy should consist of exactly n brand new nodes, where each new node has its value set to the value of its corresponding original node. Both the next and random pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. None of the pointers in the new list should point to nodes in the original list.

For example, if there are two nodes X and Y in the original list, where X.random --> Y, then for the corresponding two nodes x and y in the copied list, x.random --> y.

Return the head of the copied linked list.

The linked list is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:

Your code will only be given the head of the original linked list.

Example 1:

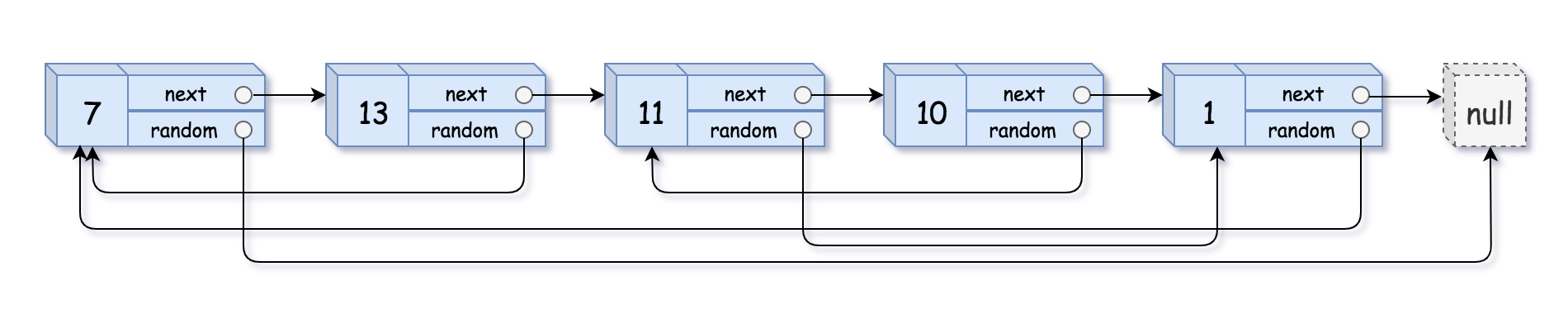
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]

Example 2:

Input: head = [[1,1],[2,1]]
Output: [[1,1],[2,1]]

Example 3:

Input: head = [[3,null],[3,0],[3,null]]
Output: [[3,null],[3,0],[3,null]]

Constraints:

Solution 

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;

    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/

class Solution {
public:
    Node* copyRandomList(Node* head) {
        std::ios::sync_with_stdio(false);

                if (!head) return nullptr;

        Node* curr = head;
        while (curr) {
            Node* new_node = new Node(curr->val);
            new_node->next = curr->next;
            curr->next = new_node;
            curr = new_node->next;
        }

        curr = head;
        while (curr) {
            if (curr->random) {
                curr->next->random = curr->random->next;
            }
            curr = curr->next->next;
        }

        Node* old_head = head;
        Node* new_head = head->next;
        Node* curr_old = old_head;
        Node* curr_new = new_head;

        while (curr_old) {
            curr_old->next = curr_old->next->next;
            curr_new->next = curr_new->next ? curr_new->next->next : nullptr;
            curr_old = curr_old->next;
            curr_new = curr_new->next;
        }

        return new_head;
    }
};

Complexity Analysis 

| Algorithm                                | Time Complexity | Space Complexity |
| ---------------------------------------- | --------------- | ---------------- |
| Two-pointer traversal with Graph cloning | O(n)            | O(n)             |

Explanation

Intial Thoughts

When approaching this problem, it’s essential to consider the interdependencies between the nodes due to the random pointers. One approach is to create a simple hash map that maps the original nodes to their deep copies. However, this approach has a time complexity of O(n) and space complexity of O(n) as well. Alternatively, we can think of a strategy to create a copy of each node in the original list, altering the next pointers to accommodate new nodes while preserving the original connections. We can differentiate the cloned nodes by setting the next pointer of the original node to the cloned node, a strategy referred to as ‘weaving the clone list with the original list’. We then fix the random pointers of the cloned nodes by following the original connections. This approach only involves changing the original list temporarily and finally decouples the cloned list from the original list, ensuring that no references from the cloned list to the original nodes are left. The time complexity for this approach remains O(n) and the space complexity is also O(1), not including the output space for the cloned list. Considering we are dealing with a deeply complex data structure like linked lists and want to optimize the solution for both space and time, the two-pass approach strategy seems the most fitting. We can apply this strategy to break down the original problem and finally restore the cloned version of the linked list.

Intuitive Analysis

To develop the problem-solving intuition, think of linked lists as forming an intricate dance. First, we fix the ’next step’ for each pair of nodes. Going forward, notice how original pointers were pointing not to their own similar pairs but individual nodes instead, then replicate that in the next step for the deep copied nodes. Lastly, understand that even restoring original connections by going back and fixing them, a new, independent network has been created that mirrors the original but exists independently in one whole piece.

1. Intuition

2. Implementation

Complexity Analysis

Time Complexity:

Space Complexity:

Footnote

This question is rated as Medium difficulty.

Hints

Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, ensure you are not making multiple copies of the same node.

You may want to use extra space to keep old_node —> new_node mapping to prevent creating multiple copies of the same node.

We can avoid using extra space for old_node —> new_node mapping by tweaking the original linked list. Simply interweave the nodes of the old and copied list. For example: Old List: A –> B –> C –> D InterWeaved List: A –> A’ –> B –> B’ –> C –> C’ –> D –> D’

The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers.

Similar Questions:

Title URL Difficulty
Clone Graph https://leetcode.com/problems/clone-graph Medium
Clone Binary Tree With Random Pointer https://leetcode.com/problems/clone-binary-tree-with-random-pointer Medium
Clone N-ary Tree https://leetcode.com/problems/clone-n-ary-tree Medium