The Indian Engineer

Problem 108 Convert Sorted Array to Binary Search Tree

Posted on 2 mins

Recursion Binary-Tree Binary-Search-Tree

Table of Contents

Problem Statement

Link - Problem 108

Question

Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.

A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.

Example 1

img1 img2 

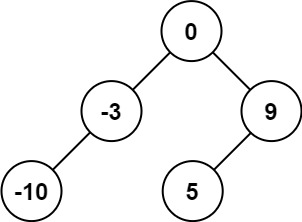
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:

Example 2

img3 

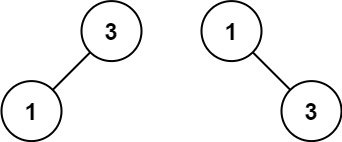
Input: nums = [1,3]
Output: [3,1]
Explanation: [1,null,3] and [3,1] are both height-balanced BSTs.

Constraints

Solution 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* helper(vector<int>& nums, int l, int r){
        if(l>r)
            return nullptr;
        int mid = (l+r)/2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums,l,mid-1);
        root->right = helper(nums,mid+1,r);

        return root;
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        int size = nums.size()-1;
        TreeNode * root = helper(nums,0,size);
        return root;
    }
};

Complexity Analysis 

| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| Recursion | O(N)            | O(N)             |

Explanation

1. Intuition 

- In a sorted array, the middle element is the root of the tree.
- Sorted array is same as inorder traversal of the binary search tree.
- So, we can recursively build the tree by finding the middle element and then recursively build the left and right subtree.
- Assign the left and right child of the root node to the left and right subtree.
- Left sub tree will be from 0 to mid-1 and right subtree will be from mid+1 to n.

2. Implementation 

- Define a function `helper` which takes the sorted array and the left and right index.
- If left index is greater than right index, return nullptr.
- Find the middle element of the range `l` to `r`.
- Create a new node with the middle element as the value.
- Recursively call the helper function for the left and right subtree.
- Assign the left and right child of the root node to the left and right subtree.
- Return the root node.