• Posts

Problem 1074 Number of Submatrices That Sum to Target

Problem Statement

Link - Problem 1074

Question

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

Example 1:

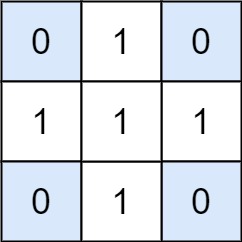
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Example 3:

Input: matrix = [[904]], target = 0
Output: 0

Constraints:

• 1 <= matrix.length <= 100
• 1 <= matrix[0].length <= 100
• -1000 <= matrix[i][j] <= 1000
• -10^8 <= target <= 10^8

Solution

class Solution {
public:
    int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
        int numRows = matrix.size();
        int numCols = matrix[0].size();

        vector<vector<int>> prefixSum(numRows + 1, vector<int>(numCols + 1, 0));

        for (int row = 0; row < numRows; ++row) {
            for (int col = 0; col < numCols; ++col) {
                prefixSum[row + 1][col + 1] = prefixSum[row][col + 1] + prefixSum[row + 1][col] - prefixSum[row][col] + matrix[row][col];
            }
        }

        int count = 0;
        for (int row1 = 0; row1 < numRows; ++row1) {
            for (int row2 = row1 + 1; row2 <= numRows; ++row2) {
                unordered_map<int, int> counter;
                counter[0] = 1;
                for (int col = 1; col <= numCols; ++col) {
                    int currSum = prefixSum[row2][col] - prefixSum[row1][col];
                    count += counter[currSum - target];
                    ++counter[currSum];
                }
            }
        }
        return count;
    }
};

Complexity Analysis

| Algorithm                | Time Complexity | Space Complexity |
| ------------------------ | --------------- | ---------------- |
| Hash Map with Prefix Sum | O(n^3 log n)    | O(n)             |

Explanation

Intial Thoughts

To approach this problem, first think about the structure of a matrix and how submatrices are formed. Consider how you can efficiently calculate the sum of each submatrix. Note that the problem statement involves both positive and negative numbers, which can result in both positive and negative sums. Think about how you can keep track of the sums that have been seen so far. It might be useful to use a prefix sum array or a hash map to store intermediate results. Break down the problem into smaller sub-problems, such as calculating the sum of submatrices with a specific row or column range.

Intuitive Analysis

To intuitively solve this problem, think of the prefix sum array as a tool to efficiently calculate the sum of any submatrix. Imagine a sliding window approach where you are moving the top and bottom boundaries of the submatrix, and for each position, you are calculating the sum of the submatrix. Use a hash map to store the frequency of each sum that has been seen so far. The key insight is that the number of submatrices that sum to the target is equal to the number of times the target minus the current sum is seen in the hash map. By using this approach, you can avoid recalculating the sum of submatrices and reduce the time complexity.

1. Intuition

• The problem can be solved by using a prefix sum approach to efficiently calculate the sum of any submatrix.
• The prefix sum approach allows us to calculate the sum of a submatrix in constant time, which is crucial for achieving an efficient solution.
• We can use a hashmap to store the cumulative sum of each row and the frequency of each sum, which enables us to count the number of submatrices with a given sum in linear time.
• The key insight is to fix the top and bottom rows of the submatrix and then iterate over all possible left and right columns.
• This approach ensures that we consider all possible submatrices and count the ones with the target sum.
• The time complexity of this approach is O(n^3), where n is the number of rows in the matrix.
• The space complexity is O(n), which is used to store the prefix sum and the hashmap.

2. Implementation

• We initialize a 2D array prefixSum to store the prefix sum of the matrix, where prefixSum[i][j] represents the sum of all elements in the submatrix from (0, 0) to (i, j).
• We calculate the prefix sum using the formula prefixSum[i][j] = prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1] + matrix[i][j].
• We iterate over all possible top and bottom rows of the submatrix using two nested loops.
• For each pair of top and bottom rows, we iterate over all possible left columns and calculate the cumulative sum of the submatrix.
• We use a hashmap counter to store the frequency of each cumulative sum and count the number of submatrices with the target sum.
• We update the count by adding the frequency of the cumulative sum minus the target sum to the count.
• Finally, we return the count as the result.

Complexity Analysis

Time Complexity:

• The algorithm starts by calculating the prefix sum of the matrix in O(numRows _ numCols) time. However, this is dominated by the nested for loops over all possible submatrices (row1 and row2), each taking O(numCols) time. Hence, the overall time complexity becomes O(numRows^2 _ numCols). Additionally, an unordered*map is used to keep track of the cumulative sum, contributing a O(log numCols) factor. Therefore, the total time complexity is O(numRows^2 * numCols _ log numCols) which can be simplified to O(n^3 log n) where n is the number of rows (or columns) of the matrix.
• The innermost for loop at for (int col = 1; col <= numCols; ++col) iterates over each column, and the counter[currSum - target] operation within the loop contributes a significant amount to the time complexity. However, as an unordered_map is used, this operation takes constant time and does not affect the overall time complexity significantly.
• The use of nested loops and the contribution of the unordered_map can be justified using Big O notation. Since Big O provides an upper bound on the time complexity, and the given algorithm consists of operations that take O(n^3 log n) time in the worst case, the algorithm is classified as O(n^3 log n).

Space Complexity:

• The given algorithm requires extra space to store the prefix sum matrix (prefixSum) and an unordered_map (counter). The prefix sum matrix takes O(numRows * numCols) space since it has an extra row and column. Hence, this is the dominant contributor to the space complexity.
• The unordered_map (counter) is used to store cumulative sums encountered so far. Since the map stores at most numCols entries in the worst case, the space complexity of the map can be considered as O(numCols). However, it is often noted that this growth rate is much slower than the growth rate of prefixSum.
• Given that the prefix sum matrix takes O(numRows * numCols) space, we can conclude the space complexity of the given algorithm is indeed O(n^2), where n is the number of rows (or columns) of the matrix, rather than O(n).

Footnote

This question is rated as Hard difficulty.

Hints

Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time. Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window.

Similar Questions: