• Leetcode POTDs

Problem 951 Flip Equivalent Binary Trees

Problem Statement

Link - Problem 951

Question

For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.

A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.

Given the roots of two binary trees root1 and root2, return true if the two trees are flip equivalent or false otherwise.

Example 1

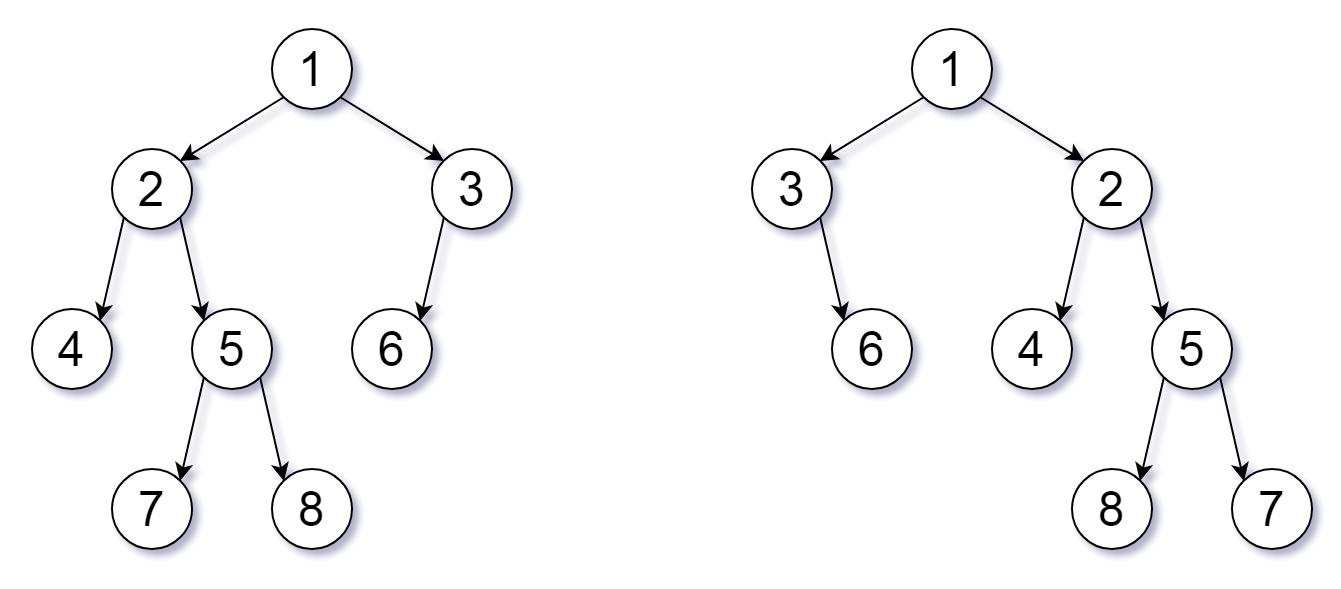
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.

Example 2

Input: root1 = [], root2 = []
Output: true

Example 3

Input: root1 = [], root2 = [1]
Output: false

Constraints

• The number of nodes in each tree is in the range [0, 100].
• Each tree will have unique node values in the range [0, 99].

Solution

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    bool flipEquiv(TreeNode* root1, TreeNode* root2) {
        if (root1 == NULL || root2 == NULL)
            return root1 == root2;
        if (root1->val != root2->val)
            return false;
        return (flipEquiv(root1->left, root2->left) && flipEquiv(root1->right, root2->right)) ||
                flipEquiv(root1->left, root2->right) && flipEquiv(root1->right, root2->left);
    }
};

Complexity Analysis

| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| DFS       | O(N)            | O(N)             |

Explanation

1. Intuition: Tree Isomorphism with Controlled Transformations

The problem of flip-equivalent binary trees is fundamentally about tree isomorphism with a specific allowed transformation - the ability to swap left and right children at any node. This transforms the traditional tree equality problem into a more nuanced structural equivalence problem.

Core Concept

The fundamental insight lies in understanding that two trees can be structurally equivalent even if their current arrangement differs. At each node, we have two valid states for comparison:

1. Direct structural match (left-to-left, right-to-right)
2. Crossed structural match (left-to-right, right-to-left)

2. Mathematical Proof of Correctness

Let’s establish the correctness through formal proof:

1. Formal Definition:

   $$ \begin{aligned} & \text{Let } T_1, T_2 \text{ be binary trees} \\ & T_1 \equiv T_2 \iff \exists \text{ sequence of flips } F = \{f_1, f_2, ..., f_n\} \\ & \text{such that } F(T_1) = T_2 \\ & \text{where } f_i: V \rightarrow \{0,1\} \text{ represents a flip decision at node } v \in V \end{aligned} $$

2. Recursive Equivalence Relation:

   $$ \begin{aligned} & \text{flipEquiv}(n_1, n_2) \iff \\ & \begin{cases} \text{true} & \text{if } n_1 = n_2 = \text{null} \\ \text{false} & \text{if } n_1 = \text{null} \oplus n_2 = \text{null} \\ \text{false} & \text{if } n_1.\text{val} \neq n_2.\text{val} \\ E(n_1, n_2) & \text{otherwise} \end{cases} \end{aligned} $$

Where E(n₁, n₂) is defined as:

3. Time Complexity Analysis:

   $$ \begin{aligned} T(n) &= 2T(n/2) + O(1) \\ &= O(n) \text{ by Master Theorem} \end{aligned} $$

4. Space Complexity on Recursion Stack:

   $$ S(n) = O(h) \text{ where h is the height of the smaller tree} $$

3. Implementation Analysis

bool flipEquiv(TreeNode* root1, TreeNode* root2) {
    if (root1 == NULL || root2 == NULL)
        return root1 == root2;
    if (root1->val != root2->val)
        return false;
    return (flipEquiv(root1->left, root2->left) &&
            flipEquiv(root1->right, root2->right)) ||
           (flipEquiv(root1->left, root2->right) &&
            flipEquiv(root1->right, root2->left));
}

4. Optimality Proof

Let’s prove that our solution is optimal:

5. Edge Case Analysis

The solution handles all edge cases through its recursive definition:

Technical Note: This mathematical formulation demonstrates how recursive tree equivalence checking under constrained transformations can be elegantly expressed and proven correct using formal mathematics. The solution leverages the principle that local structural equivalence implies global structural equivalence under the given transformation rules.