Leetcode POTDs

Problem 790 Domino and Tromino Tiling

Posted on May 5, 2025 6 mins

Dynamic-Programming

Table of Contents

Problem Statement

Link - Problem 790

Question

You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

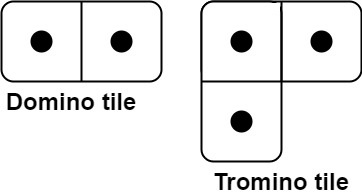
Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 10⁹ + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

Example 1:

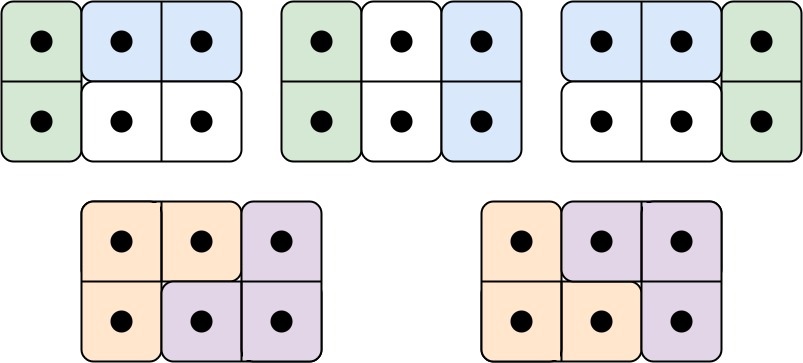
Input: n = 3
Output: 5
Explanation: The five different ways are show above.

Example 2:

Input: n = 1
Output: 1

Constraints:

1 <= n <= 1000

Solution

class Solution {
public:
    int numTilings(int n) {
        const int MOD = 1e9 + 7;
        vector<long long> dp(max(4, n + 1), 0);
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 5;

        for (int i = 4; i <= n; ++i) {
            dp[i] = (2 * dp[i - 1] + dp[i - 3]) % MOD;
        }

        return dp[n];
    }
};

Complexity Analysis

| Algorithm           | Time Complexity | Space Complexity |
| ------------------- | --------------- | ---------------- |
| Dynamic Programming | O(n)            | O(n)             |

Explanation

Intial Thoughts

To solve this problem, consider the board as a series of units that need to be covered. Think about how each type of tile can cover these units and how the arrangement of tiles affects the overall number of ways to tile the board. Key points include: breaking down the problem into smaller parts, understanding how tiles can be arranged, recognizing patterns in tiling, considering the role of the tromino shape, and identifying a method to keep track of the number of ways to tile the board. Additionally, consider the constraints and how they impact the solution, such as the size of the board and the available tiles.

Intuitive Analysis

To intuitively solve this problem, think about the tiling process step by step, focusing on how each new tile adds to the existing arrangement. Consider the following points: the base cases for small boards, how adding a new column to the board changes the possibilities, the relationship between the number of ways to tile a board of size n and the number of ways to tile smaller boards, the role of dynamic programming in tracking these relationships, and how to use these insights to calculate the number of ways to tile a board of any given size. Furthermore, consider the importance of avoiding overcounting and ensuring that each arrangement is unique, and how the modulo operation can help manage large numbers of possibilities.

1. Intuition

The problem can be solved using dynamic programming, where we build up a solution to the larger problem from the solutions of smaller sub-problems
We need to consider the number of ways to tile a 2 x n board, which can be broken down into smaller sub-problems of tiling a 2 x (n-1), 2 x (n-2), and 2 x (n-3) board
The key insight is that a 2 x n board can be tiled by adding a domino to a 2 x (n-1) board, or by adding a tromino to a 2 x (n-3) board
We also need to consider the base cases, where n is 0, 1, 2, or 3, and there is only one way to tile a 2 x 0 board (i.e., not tiling it at all), one way to tile a 2 x 1 board, two ways to tile a 2 x 2 board, and five ways to tile a 2 x 3 board
The problem requires us to return the number of ways to tile the board modulo 10^9 + 7, to avoid overflow
The dynamic programming approach allows us to efficiently compute the solution for larger values of n, by building up the solution from the solutions of smaller sub-problems
The time complexity of the solution is O(n), and the space complexity is O(n), as we need to store the number of ways to tile a 2 x i board for all i from 0 to n

2. Implementation

We initialize a vector dp of size n+1, where dp[i] represents the number of ways to tile a 2 x i board
We set the base cases, where dp[0] = 1, dp[1] = 1, dp[2] = 2, and dp[3] = 5
We then iterate from i = 4 to n, and for each i, we calculate dp[i] as (2 * dp[i-1] + dp[i-3]) % MOD, where MOD is 10^9 + 7
The (2 * dp[i-1] + dp[i-3]) expression represents the number of ways to tile a 2 x i board, by adding a domino to a 2 x (i-1) board, or by adding a tromino to a 2 x (i-3) board
The % MOD expression ensures that the result is taken modulo 10^9 + 7, to avoid overflow
Finally, we return dp[n], which represents the number of ways to tile a 2 x n board
The const int MOD = 1e9 + 7 line defines the modulo value, and the vector<long long> dp(max(4, n + 1), 0) line initializes the dp vector

Complexity Analysis

Time Complexity:

The algorithm iterates from i = 4 to n using a single loop, resulting in a linear number of operations. The dominant operation is the calculation of dp[i] which involves constant time arithmetic operations, thus the overall time complexity remains linear.
For each iteration, the algorithm performs a constant amount of work, with no nested loops or recursive calls that depend on the input size n. This justifies a time complexity of O(n), where n is the input size.
Considering the best, average, and worst cases, the time complexity remains O(n) as the loop always runs from 4 to n, with no conditional statements that could alter the number of iterations based on the input.

Space Complexity:

The algorithm uses a vector dp of size max(4, n + 1) to store the results of subproblems, resulting in a space complexity that scales linearly with the input size n.
The space complexity is dominated by the dp vector, which requires O(n) space to store the solutions to subproblems. This allows the algorithm to avoid redundant calculations and improve performance.
The space complexity remains O(n) even in the best, average, and worst cases, as the size of the dp vector is directly proportional to the input size n.

Footnote

This question is rated as Medium difficulty.