• Leetcode POTDs

Problem 773 Sliding Puzzle

Problem Statement

Link - Problem 773

Question

On an 2 x 3 board, there are five tiles labeled from 1 to 5, and an empty square represented by 0. A move consists of choosing 0 and a 4-directionally adjacent number and swapping it.

The state of the board is solved if and only if the board is [[1,2,3],[4,5,0]].

Given the puzzle board board, return the least number of moves required so that the state of the board is solved. If it is impossible for the state of the board to be solved, return -1.

Example 1:

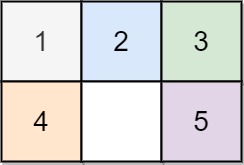
Input: board = [[1,2,3],[4,0,5]]
Output: 1
Explanation: Swap the 0 and the 5 in one move.

Example 2:

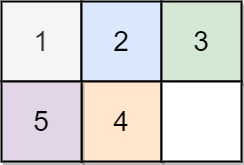
Input: board = [[1,2,3],[5,4,0]]
Output: -1
Explanation: No number of moves will make the board solved.

Example 3:

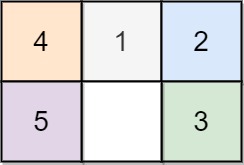
Input: board = [[4,1,2],[5,0,3]]
Output: 5
Explanation: 5 is the smallest number of moves that solves the board.
An example path:
After move 0: [[4,1,2],[5,0,3]]
After move 1: [[4,1,2],[0,5,3]]
After move 2: [[0,1,2],[4,5,3]]
After move 3: [[1,0,2],[4,5,3]]
After move 4: [[1,2,0],[4,5,3]]
After move 5: [[1,2,3],[4,5,0]]

Constraints:

• board.length == 2
• board[i].length == 3
• 0 <= board[i][j] <= 5
• Each value board[i][j] is unique.

Solution

class Solution {
public:
    int slidingPuzzle(vector<vector<int>>& board) {

        vector<vector<int>> directions = {{1, 3}, {0, 2, 4}, {1, 5},
                                          {0, 4}, {1, 3, 5}, {2, 4}};

        string target = "123450";
        string start_state;
        for (int i = 0; i < board.size(); i++) {
            for (int j = 0; j < board[0].size(); j++) {
                start_state += to_string(board[i][j]);
            }
        }

        unordered_set<string> visited;
        queue<string> queue;
        queue.push(start_state);
        visited.insert(start_state);

        int moves = 0;

        while (!queue.empty()) {
            int size = queue.size();
            while (size > 0) {
                string curr_state = queue.front();
                queue.pop();

                if (curr_state == target) {
                    return moves;
                }

                int zeroPos = curr_state.find('0');
                for (int newPos : directions[zeroPos]) {
                    string next_state = curr_state;
                    swap(next_state[zeroPos], next_state[newPos]);

                    if (visited.count(next_state))
                        continue;

                    visited.insert(next_state);
                    queue.push(next_state);
                }
                size--;
            }
            moves++;

        }
        return -1;
    }
};

Complexity Analysis

| Algorithm                                           | Time Complexity | Space Complexity |
| --------------------------------------------------- | --------------- | ---------------- |
| Breadth-First Search with queue (Uninformed search) | O(b^d)          | O(b^d)           |

Explanation

1. Intuition

• The problem can be solved using a breadth-first search (BFS) algorithm.
• The BFS algorithm is suitable for this problem because it allows us to explore all possible states of the board in a level-order manner.
• We can represent each state of the board as a string, where the digits 1-5 and 0 represent the tiles and the empty space, respectively.
• The goal state is the string 123450, which represents the solved board.
• We can use a queue to keep track of the states to be explored, and a set to keep track of the visited states.
• The algorithm terminates when it finds the goal state or when the queue is empty, indicating that it is impossible to solve the board.

2. Implementation

• The directions vector is used to represent the possible moves from each position on the board, directions = {{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}};
• The target string represents the goal state, string target = '123450';
• The start_state string represents the initial state of the board, which is constructed by iterating over the board vector.
• The visited set is used to keep track of the visited states, unordered_set<string> visited;
• The queue is used to keep track of the states to be explored, queue<string> queue;
• The algorithm uses a while loop to explore the states in the queue, and a nested while loop to explore the neighbors of each state.
• The moves variable is used to keep track of the number of moves, int moves = 0;

Complexity Analysis

Time Complexity:

• The time complexity is determined by the Breadth-First Search (BFS) algorithm used to explore all possible states of the sliding puzzle. The BFS algorithm has a time complexity of O(b^d), where b is the branching factor (i.e., the average number of possible moves from a given state) and d is the depth of the search tree.
• The dominant operation in this algorithm is the expansion of the current state into all possible next states, which is performed in the loop for (int newPos : directions[zeroPos]). This operation has a time complexity of O(b), as there are on average b possible moves from a given state.
• The entire search tree is traversed, resulting in a total time complexity of O(b^d), as each node in the tree is visited once. This is justified by the fact that the search is performed level by level, and all nodes at each level are visited before moving on to the next level.

Space Complexity:

• The space complexity is determined by the need to store all visited states in the visited unordered set and the current queue of states to be visited.
• The space required to store the visited states is O(b^d), as each state is stored once in the visited set, and there are b^d possible states in the search tree.
• The space required to store the current queue of states is also O(b^d), as in the worst case, the queue will contain all states at the deepest level of the search tree. Therefore, the overall space complexity is O(b^d).

Footnote

This question is rated as Hard difficulty.

Hints

Perform a breadth-first-search, where the nodes are the puzzle boards and edges are if two puzzle boards can be transformed into one another with one move.