• Leetcode POTDs

Problem 48 Rotate Image

Problem Statement

Link - Problem 48

Question

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

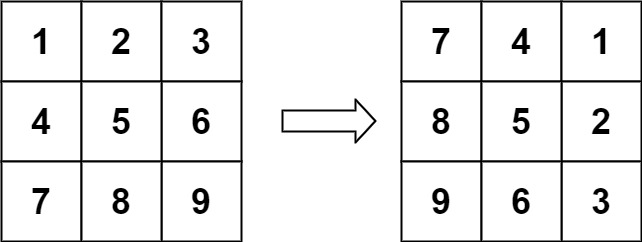
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

Example 2:

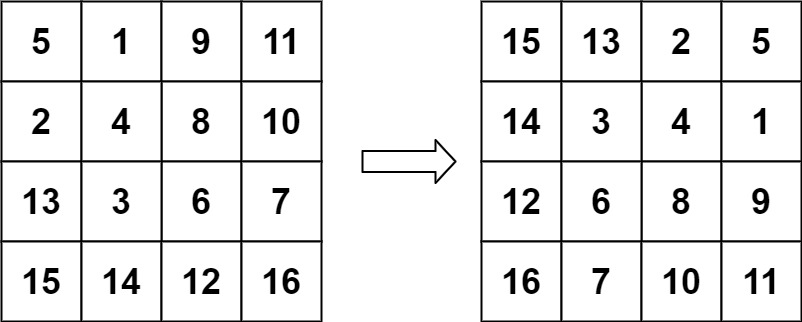
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

Solution

class Solution {
public:
  void rotate(vector<vector<int>>& matrix) {
    int n = matrix.size();
    int temp;
    for(int i = 0; i < n / 2; i++)
        for(int j = i; j < n - i - 1; j++)
        {
            temp = matrix[i][j];
            matrix[i][j] = matrix[n - j - 1][i];
            matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
            matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
            matrix[j][n - i - 1] = temp;
        }
}

};

Complexity Analysis

| Algorithm                        | Time Complexity | Space Complexity |
| -------------------------------- | --------------- | ---------------- |
| Layered in-place matrix rotation | O(n^2)          | O(1)             |

Explanation

Intial Thoughts

To approach this problem, think of the matrix as layers. Try visualizing the image and see how each layer would be affected. Focus on how to shift each layer without tampering with the original. To start, analyze how swapping the corner elements might work, this is essentially shifting layers and corners around. One method to attempt is transposing the matrix, followed by reversing each row for a 90 degree clockwise rotation. This can also help in simplifying how we should approach this problem. Another option is grouping the corners with edges which may require multiple nested loops, hence considering the algorithmic complexity during coding. Understanding these concepts helps us design our algorithm for achieving 90 degree rotation successfully. Recognize that in-place means altering current structure without requiring new structures.

Intuitive Analysis

When visualizing the rotation, it becomes intuitive that rotating each 2 x 2 cell within the matrix first will bring us halfway towards achieving our result. Think of the operation on a smaller scale: consider what happens when you rotate a single element – it moves to its adjacent element and then is swapped again. To solve this problem think in ‘cycles’ how each corner moves, to the opposite corner i.e., shifting 90 degrees clockwise and finally each row shifted with all corner elements now having the old element values changed. In order to finalize, ensure that it stays in same row yet each column gets moved up one and new rotated corners added in.

1. Intuition

• The problem requires rotating a 2D matrix by 90 degrees clockwise in-place.
• To achieve this, we can use a layer-by-layer approach, starting from the outermost layer and moving inwards.
• Each layer is a square ring, and we can rotate the elements in each ring independently.
• The key insight is to recognize that each element in the ring can be rotated by swapping it with the corresponding elements in the other three positions of the ring.
• This approach ensures that the rotation is done in-place, without allocating additional memory.
• The time complexity of this approach is O(n^2), where n is the size of the matrix.
• The space complexity is O(1), since we are only using a constant amount of extra memory to store the temporary variable.

2. Implementation

• We start by getting the size of the matrix using int n = matrix.size();.
• We then iterate over each layer of the matrix using two nested loops: for(int i = 0; i < n / 2; i++) and for(int j = i; j < n - i - 1; j++).
• Inside the inner loop, we swap the elements in the current ring using a temporary variable temp.
• We first store the top-left element in temp, then move the top-right element to the top-left position, the bottom-right element to the top-right position, and so on.
• We use the following assignments to swap the elements: matrix[i][j] = matrix[n - j - 1][i];, matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];, matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];, and matrix[j][n - i - 1] = temp;.
• We repeat this process for each layer of the matrix until we have rotated all the elements.

Complexity Analysis

Time Complexity:

• The time complexity analysis begins with the two nested loops for(int i = 0; i < n / 2; i++) and for(int j = i; j < n - i - 1; j++), which both run approximately n/2 and n-i-1 times respectively. This results in a total of roughly n*(n-1)/2 iterations.
• The dominant operations within the loops are the assignments and swaps of elements within the matrix, which occur in constant time O(1). As such, each iteration of the loops contributes to the overall time complexity in linear fashion.
• Taking into account the approximations and considering the Big O notation’s focus on the worst case, the n*(n-1)/2 iterations can be simplified to O(n^2), since the n-1 is a constant factor in this context and is thus omitted in the final classification.

Space Complexity:

• This solution uses in-place matrix rotation, requiring no additional space that scales with input size n, since only a constant amount of space is used to store the temporary variable temp.
• The given array is not duplicated or transposed; instead, elements are rotated within their current bounds, thus removing the need for extra memory allocations that would increase with n.
• Considering the constant usage of memory regardless of input size, this solution’s space complexity is classified as O(1)

Footnote

This question is rated as Medium difficulty.

Similar Questions: