Problem 3208 Alternating Groups II
Table of Contents
Problem Statement
Link - Problem 3208
Question
There is a circle of red and blue tiles. You are given an array of integers colors and an integer k. The color of tile i is represented by colors[i]:
colors[i] == 0means that tileiis red.colors[i] == 1means that tileiis blue.
An alternating group is every k contiguous tiles in the circle with alternating colors (each tile in the group except the first and last one has a different color from its left and right tiles).
Return the number of alternating groups.
Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.
Example 1:
Input: colors = [0,1,0,1,0], k = 3
Output: 3
Explanation:
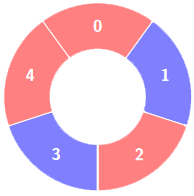
Alternating groups:
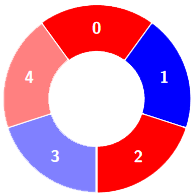
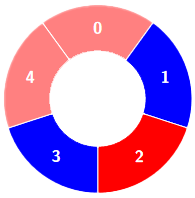
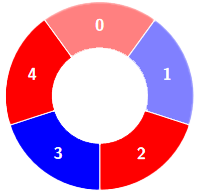
Example 2:
Input: colors = [0,1,0,0,1,0,1], k = 6
Output: 2
Explanation:

Alternating groups:


Example 3:
Input: colors = [1,1,0,1], k = 4
Output: 0
Explanation:
Constraints:
3 <= colors.length <= 1050 <= colors[i] <= 13 <= k <= colors.length
Solution
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
for (int i = 0; i < k - 1; ++i)
colors.push_back(colors[i]);
int res = 0;
int cnt = 1;
for (int i = 1; i < colors.size(); ++i) {
if (colors[i] != colors[i - 1])
++cnt;
else
cnt = 1;
if (cnt >= k)
++res;
}
return res;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| ---------------------------------------------- | --------------- | ---------------- |
| Modded Sliding Window Enumeration and Counting | O(n) | O(k) |
Explanation
Intial Thoughts
To approach this problem, first understand that we have a circular arrangement of red and blue tiles. An alternating group is formed when k contiguous tiles have alternating colors. Since the arrangement is circular, we need to consider the last and first tiles as adjacent. Initially, we cannot directly analyze the given array because of its circular nature. We need to consider the given array as a non-circular array by either making a copy or adding the first elements again at the end of the array to make it look like the circle. Then, we can iterate through the array to check for alternating groups.
Intuitive Analysis
An intuitive way to solve this problem is to think of it as identifying a pattern in the array. To identify an alternating pattern, we can simply check for adjacent tiles with different colors. We can maintain a counter to keep track of the number of continuous alternating tiles we have seen so far. As soon as we encounter a tile with the same color as its previous one, we can reset the counter. We can then check if the counter is equal to or greater than k. If yes, we have identified an alternating group and increment our result.
1. Intuition
- The problem asks for the number of alternating groups in a circular array of red and blue tiles.
- To solve this problem, we can extend the given array by appending the first k-1 elements to the end.
- This allows us to treat the circular array as a linear array and simplify the problem.
- We can then iterate through the extended array and count the number of alternating groups.
- An alternating group is formed when we have k consecutive tiles with alternating colors.
- We can use a counter to keep track of the length of the current alternating group.
- When the counter reaches k, we increment the result and reset the counter.
2. Implementation
- We start by extending the given array using a loop:
for (int i = 0; i < k - 1; ++i) colors.push_back(colors[i]); - We then initialize two variables:
resto store the result andcntto keep track of the length of the current alternating group. - We iterate through the extended array using a loop:
for (int i = 1; i < colors.size(); ++i) - Inside the loop, we check if the current tile has a different color than the previous tile:
if (colors[i] != colors[i - 1]) - If the colors are different, we increment the counter:
++cnt; - If the colors are the same, we reset the counter:
cnt = 1; - We also check if the counter has reached k:
if (cnt >= k) - If it has, we increment the result:
++res;
Complexity Analysis
Time Complexity:
- The time complexity of this algorithm is influenced by two key loops:
for (int i = 0; i < k - 1; ++i)andfor (int i = 1; i < colors.size(); ++i). The first loop iteratesk - 1times, resulting in O(k) complexity. - However, since
colors.push_back(colors[i])adds elements to the vector and makes the second loop’s size dependent onk, the dominant operation becomes the iteration through the colors vector in the second loop. - This gives us a linear time complexity because the two main loops together perform a total of
n + k - 1operations, wherenis the original number of colors.
Space Complexity:
- The primary memory usage comes from the expansion of the
colorsvector byk - 1elements, done withcolors.push_back(colors[i]) - This expansion is done
k - 1times, meaning the space used grows by a constant factork, independent of the original vector sizen. - Given this modification to the original data, we deduce that the space complexity directly relates to the
kfactor since that defines how extensively the space is increased relative to the originalcolorssize.
Footnote
This question is rated as Medium difficulty.
Hints
Try to find a tile that has the same color as its next tile (if it exists).
Then try to find maximal alternating groups by starting a single for loop from that tile.