• Leetcode POTDs

Problem 2924 Find Champion II

Problem Statement

Link - Problem 2924

Question

There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.

You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.

A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a.

Team a will be the champion of the tournament if there is no team b that is stronger than team a.

Return the team that will be the champion of the tournament if there is a unique champion, otherwise, return -1.

Notes

• A cycle is a series of nodes a1, a2, ..., an, an+1 such that node a1 is the same node as node an+1, the nodes a1, a2, ..., an are distinct, and there is a directed edge from the node ai to node ai+1 for every i in the range [1, n].
• A DAG is a directed graph that does not have any cycle.

Example 1:

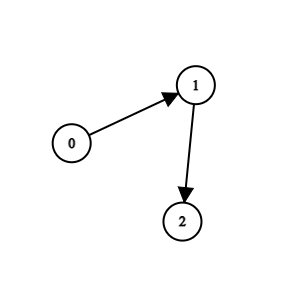
Input: n = 3, edges = [[0,1],[1,2]]
Output: 0
Explanation: Team 1 is weaker than team 0. 
Team 2 is weaker than team 1. 
So the champion is team 0.

Example 2:

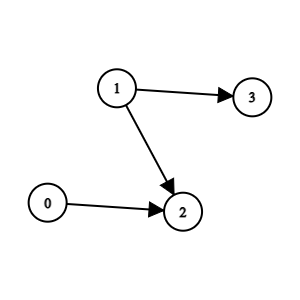
Input: n = 4, edges = [[0,2],[1,3],[1,2]]
Output: -1
Explanation: Team 2 is weaker than team 0 and team 1. 
Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams.
So the answer is -1.

Constraints:

• 1 <= n <= 100
• m == edges.length
• 0 <= m <= n * (n - 1) / 2
• edges[i].length == 2
• 0 <= edge[i][j] <= n - 1
• edges[i][0] != edges[i][1]
• The input is generated such that if team a is stronger than team b, team b is not stronger than team a.
• The input is generated such that if team a is stronger than team b and team b is stronger than team c, then team a is stronger than team c.

Solution

class Solution {
public:
    int findChampion(int n, vector<vector<int>>& edges) {
        vector<int> in_degree(n,0);
        for(auto edge:edges)
            in_degree[edge[1]]++;

        int champion = -1, count = 0;
        for(int i = 0; i<n; i++)
            if(in_degree[i]==0){
                count++;
                champion = i;
            }

        return count>1 ? -1:champion;
    }
};

Complexity Analysis

| Algorithm                         | Time Complexity | Space Complexity |
| --------------------------------- | --------------- | ---------------- |
| Directed Graph In-Degree Analysis | O(n)            | O(n)             |

Explanation

1. Intuition

• The problem can be solved by finding the node with no incoming edges in the directed graph.
• This is because a node with no incoming edges is not weaker than any other node.
• The champion of the tournament will be the node with no incoming edges.
• If there are multiple nodes with no incoming edges, then there is no unique champion.
• The problem can be solved using the concept of in-degree of a node in a graph.
• In-degree of a node is the number of edges that are incoming to the node.
• We can calculate the in-degree of each node by iterating over the edges of the graph.

2. Implementation

• Create a vector in_degree of size n to store the in-degree of each node.
• Initialize all elements of in_degree to 0.
• Iterate over the edges of the graph and increment the in-degree of the destination node of each edge.
• Use a loop to find the node with no incoming edges by checking the in_degree vector.
• If multiple nodes have no incoming edges, return -1.
• Otherwise, return the node with no incoming edges as the champion.
• The time complexity of this solution is O(n + m), where n is the number of nodes and m is the number of edges.

Complexity Analysis

Time Complexity:

• The time complexity of the solution is O(n) because it consists of two loops: the first loop for(auto edge:edges) traverses each edge once, resulting in O(n) time, where n is the number of edges, and the second loop for(int i = 0; i<n; i++) traverses each node once, resulting in O(n) time, where n is the number of nodes. Since these loops are sequential, we can add their times together.
• However, in terms of time complexity, we drop lower-order terms and ignore constants, which is why the time complexity is O(n) regardless of whether n represents nodes or edges, which we can assume will grow together in number for the purposes of this graph.
• The worst-case, average-case, and best-case times are all O(n) because both loops will always occur regardless of the input values.

Space Complexity:

• The space complexity of the solution is O(n) because it creates a vector of size n, vector<int> in_degree(n,0), to store in-degrees for each node.
• The size of the created data structure grows directly with input size (the number of nodes), justifying the space complexity classification.
• Regardless of whether the graph is highly connected or minimally connected, the size of the in_degree vector will always scale linearly with the number of nodes, thus we don’t have different space complexities in different scenarios.

Footnote

This question is rated as Medium difficulty.

Hints

The champion(s) should have in-degree 0 in the DAG.