• Leetcode POTDs

Problem 2807 Insert Greatest Common Divisors in Linked List

Problem Statement

Link - Problem 2807

Question

Given the head of a linked list head, in which each node contains an integer value.

Between every pair of adjacent nodes, insert a new node with a value equal to the greatest common divisor of them.

Return the linked list after insertion.

The greatest common divisor of two numbers is the largest positive integer that evenly divides both numbers.

Example 1

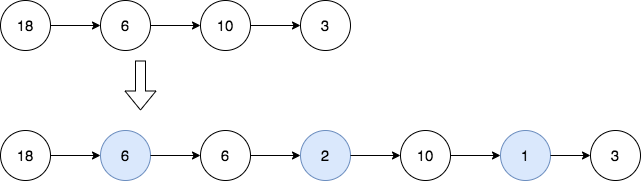
Input: head = [18,6,10,3]
Output: [18,6,6,2,10,1,3]
Explanation: The 1st diagram denotes the initial linked list
the 2nd diagram denotes the linked list after inserting the new nodes (nodes in blue are the inserted nodes).
- We insert the greatest common divisor of 18 and 6 = 6 between the 1st and the 2nd nodes.
- We insert the greatest common divisor of 6 and 10 = 2 between the 2nd and the 3rd nodes.
- We insert the greatest common divisor of 10 and 3 = 1 between the 3rd and the 4th nodes.
There are no more adjacent nodes, so we return the linked list.

Example 2

Input: head = [7]
Output: [7]
Explanation: The 1st diagram denotes the initial linked list
the 2nd diagram denotes the linked list after inserting the new nodes.
There are no pairs of adjacent nodes, so we return the initial linked list.

Constraints

• The number of nodes in the list is in the range [1, 5000].
• 1 <= Node.val <= 1000

Solution

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    int gcd(int a, int b) {
        int temp;
        if(a<b)
            return gcd(b,a);
        while (b != 0) {
            temp = a % b;
            a = b;
            b = temp;
        }
        return a;
    }
    ListNode* insertGreatestCommonDivisors(ListNode* head) {
        std::ios::sync_with_stdio(false);
        if(!head || !head->next)
            return head;

        ListNode* prev = head;
        ListNode* curr = prev->next;

        while(curr!=nullptr){
            int f = gcd(prev->val,curr->val);
            ListNode* temp = new ListNode(f,curr);
            prev->next = temp;
            prev = curr;
            curr=curr->next;
        }

        return head;

    }
};

Complexity Analysis

| Algorithm | Time Complexity   | Space Complexity |
| --------- | ----------------- | ---------------- |
| GCD       | O(log(min(a,b)))  | O(1)             |
| Traverse  | O(n)              | O(1)             |
| Total     | O(nlog(min(a,b))) | O(1)             |

Explanation

1. Intuition

The problem is straightforward. For each pair of adjacent nodes, we need to find GCD and insert a new node with the GCD value between them.

• We can find the GCD of two numbers using the Euclidean algorithm.
• Two pointers prev and curr are used to traverse the linked list.
• We iterate over the linked list until curr is not nullptr.
• For each pair of adjacent nodes, we find the GCD and insert a new node with the GCD value between them.
• We update the prev and curr pointers accordingly.

2. Implementation

- If the linked list is empty or contains only one node, we return the linked list as it is.
- Initialize two pointers `prev` and `curr` to the head of the linked list.
- Iterate over the linked list until `curr` is not `nullptr`.
- For each pair of adjacent nodes, find the GCD of their values.
- Create a new node with the GCD value and insert it between the `prev` and `curr` nodes.
- Point the `next` pointer of the `prev` node to the new node.
- Point the next of the new node to the `curr` node.
- Update the `prev` and `curr` pointers to move to the next pair of nodes.
- Return the head of the modified linked list.