Problem 2641 Cousins in Binary Tree II
Table of Contents
Problem Statement
Link - Problem 2641
Question
Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Return the root of the modified tree.
Note that the depth of a node is the number of edges in the path from the root node to it.
Example 1:
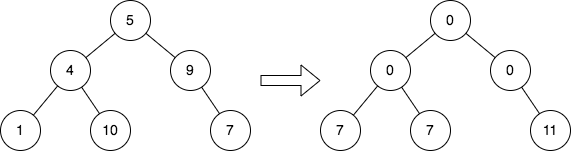
Input: root = [5,4,9,1,10,null,7] Output: [0,0,0,7,7,null,11] Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node. - Node with value 5 does not have any cousins so its sum is 0. - Node with value 4 does not have any cousins so its sum is 0. - Node with value 9 does not have any cousins so its sum is 0. - Node with value 1 has a cousin with value 7 so its sum is 7. - Node with value 10 has a cousin with value 7 so its sum is 7. - Node with value 7 has cousins with values 1 and 10 so its sum is 11.
Example 2:

Input: root = [3,1,2] Output: [0,0,0] Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node. - Node with value 3 does not have any cousins so its sum is 0. - Node with value 1 does not have any cousins so its sum is 0. - Node with value 2 does not have any cousins so its sum is 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 104
Solution
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* replaceValueInTree(TreeNode* root) {
if (!root)
return nullptr;
queue<TreeNode*> q;
int prev_level_sum = root->val;
q.push(root);
while (!q.empty()) {
int size = q.size();
int curr = 0;
while (size > 0) {
TreeNode* temp = q.front();
q.pop();
int swap_sum = (temp->left ? temp->left->val : 0) + (temp->right ? temp->right->val : 0);
if (temp->left) {
temp->left->val = swap_sum;
q.push(temp->left);
}
if (temp->right) {
temp->right->val = swap_sum;
q.push(temp->right);
}
curr += swap_sum;
temp->val = prev_level_sum - temp->val;
size--;
}
prev_level_sum = curr;
}
return root;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| --------------------- | --------------- | ---------------- |
| Level Order Traversal | O(n) | O(n) |
Explanation
1. Intuition
- The problem requires replacing each node’s value with the sum of its cousins’ values.
- Cousins are nodes at the same depth with different parents.
- A level-order traversal (BFS) can be used to process nodes at the same depth.
- For each level, calculate the sum of the node values and store it for the next level.
- For each node, calculate the sum of its children’s values and update its value with the sum of its cousins’ values.
- The root node’s value is updated with the sum of its children’s values.
- This approach ensures that each node’s value is updated with the sum of its cousins’ values.
2. Implementation
- Create a queue to store nodes for level-order traversal:
queue<TreeNode*> q; - Push the root node into the queue:
q.push(root); - Process each level of nodes:
while (!q.empty()) - Calculate the sum of the current level’s node values:
int curr = 0; - Update each node’s value with the sum of its cousins’ values:
temp->val = prev_level_sum - temp->val; - Update the sum of the current level’s node values for the next level:
prev_level_sum = curr; - Return the modified tree:
return root;
Complexity Analysis
Time Complexity:
- The algorithm involves a single pass through the binary tree, visiting each node once. This can be attributed to the use of a queue (
queue<TreeNode*> q;) that efficiently traverses all nodes level by level. - The dominant operations in the algorithm are the
pushandpopoperations in the queue (q.push(root);,TreeNode* temp = q.front();,q.pop();), which collectively take O(n) time, where n is the total number of nodes in the binary tree. - Since the algorithm visits each node exactly once, and does not have any loops or recursive calls with a depth greater than the height of the tree, its time complexity can be classified as O(n).
Space Complexity:
- The algorithm uses a queue to store nodes at each level of the tree (
queue<TreeNode*> q;). In the worst-case scenario (a complete binary tree), the space required to store all nodes at the last level is n/2, where n is the total number of nodes. - At any given time, the queue will store at most n/2 nodes, depending on the structure of the binary tree. This directly influences the algorithm’s space complexity.
- The algorithm’s use of a queue to temporarily store nodes leads to a space complexity of O(n), where n is the total number of nodes in the binary tree.
Footnote
This question is rated as Medium difficulty.
Hints
Use DFS two times.
For the first time, find the sum of values of all the levels of the binary tree.
For the second time, update the value of the node with the sum of the values of the current level - sibling node’s values.
Similar Questions:
| Title | URL | Difficulty |
|---|---|---|
| Cousins in Binary Tree | https://leetcode.com/problems/cousins-in-binary-tree | Easy |
| Maximum Level Sum of a Binary Tree | https://leetcode.com/problems/maximum-level-sum-of-a-binary-tree | Medium |