Leetcode POTDs

Problem 2583 Kth Largest Sum in a Binary Tree

Posted on Oct 22, 2024 4 mins

Binary-Tree Level-Order-Traversal Sum Bfs Queue Priority-Queue

Table of Contents

Problem Statement

Link - Problem 2583

Question

You are given the root of a binary tree and a positive integer k.

The level sum in the tree is the sum of the values of the nodes that are on the same level.

Return the kth largest level sum in the tree (not necessarily distinct). If there are fewer than k levels in the tree, return -1.

Note that two nodes are on the same level if they have the same distance from the root.

Example 1

Input: root = [5,8,9,2,1,3,7,4,6], k = 2
Output: 13
Explanation: The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.

Example 2

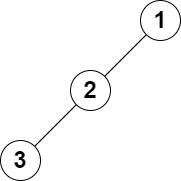
Input: root = [1,2,null,3], k = 1
Output: 3
Explanation: The largest level sum is 3.

Constraints

The number of nodes in the tree is n.
2 <= n <= 10⁵
1 <= Node.val <= 10⁶
1 <= k <= n

Solution

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    long long kthLargestLevelSum(TreeNode* root, int k) {
        priority_queue<long long, vector<long long>>pq;
        long long sum = 0;
        queue<TreeNode*>q;
        int size;
        q.push(root);
        TreeNode* temp;
        while(!q.empty()){
            size = q.size();
            while(size>0){
                temp = q.front();
                q.pop();
                sum+=temp->val;
                if(temp->left != nullptr)
                    q.push(temp->left);
                if(temp->right != nullptr)
                    q.push(temp->right);
                size--;
            }
            pq.push(sum);
            sum=0;
        }
        if(pq.size()<k)
            return -1;

        while(k>1){
            pq.pop();
            k--;
        }
        return pq.top();
    }
};

Complexity Analysis

| Algorithm      | Time Complexity | Space Complexity |
| -------------- | --------------- | ---------------- |
| BFS            | O(n)            | O(n)             |
| Priority Queue | O(nlogn)        | O(n)             |
| Total          | O(nlogn)        | O(n)             |

Explanation

1. Intuition

The question asks for the kth largest level wise sum in the binary tree.
So from the question it is clear that we need to traverse the tree level wise.
Compute the sum of the nodes at each level and store it in descending order.
Then we need to return the kth largest sum.
To make sure that we need to traverse the tree level wise we can use the BFS traversal.
We can use a queue to store the nodes at each level.
In each iteration we can compute the sum of the nodes at that level and store it in a priority_queue in descending order.
Then we need to check if the size of the priority_queue is less than k then we need to return -1.
This is because there are fewer levels than k.
If the size of the priority_queue is greater than or equal to k then we need to pop the elements from the priority_queue k-1 times.
Then return the top element of the priority_queue.

2. Implementation

- If the root is `nullptr` return `-1`.
- Create a `priority_queue` of `long long` `pq`.
- Create a variable `sum` to store the sum of the nodes at each level.
- Create a `queue` of `TreeNode*` `q`.
- Create a variable `size` to store the size of the queue.
- Push the root into the queue.
- Create a `TreeNode*` `temp`.
- Until the queue is not empty
  - Get the size of the queue.
  - Loop through the size of the queue
    - Get the front element of the queue.
    - Pop the front element of the queue.
    - Add the value of the node to the `sum`.
    - If the left child of the node is not `nullptr` push it into the queue.
    - If the right child of the node is not `nullptr` push it into the queue.
    - Decrement the size.
  - Push the `sum` into the `priority_queue`.
  - Reset the `sum` to `0`.
- If the size of the `priority_queue` is less than `k` return `-1`.
- Until `k` is not `1`
  - Pop the top element of the `priority_queue`.
  - Decrement `k`.
- Return the top element of the `priority_queue`.