• Leetcode POTDs

Problem 2458 Height of Binary Tree After Subtree Removal Queries

Problem Statement

Link - Problem 2458

Question

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

• Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.

Note:

• The queries are independent, so the tree returns to its initial state after each query.
• The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

Example 1:

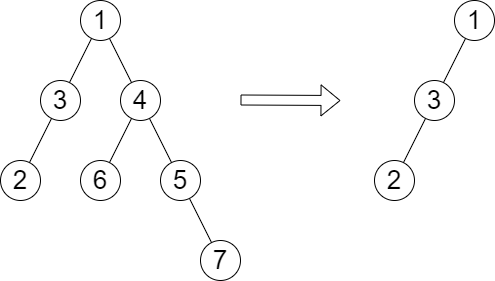
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
Output: [2]
Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.
The height of the tree is 2 (The path 1 -> 3 -> 2).

Example 2:

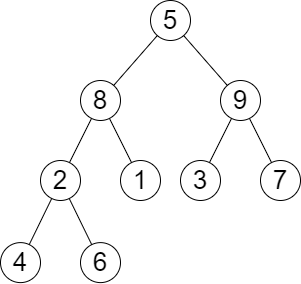
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
Output: [3,2,3,2]
Explanation: We have the following queries:
- Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
- Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
- Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
- Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= n
• All the values in the tree are unique.
• m == queries.length
• 1 <= m <= min(n, 104)
• 1 <= queries[i] <= n
• queries[i] != root.val

Solution

class Solution {
public:
    vector<int> maxHeightAfterRemoval;
    int currentMaxHeight = 0;

    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
        maxHeightAfterRemoval.resize(100001);
        traverseLeftToRight(root, 0);
        currentMaxHeight = 0;
        traverseRightToLeft(root, 0);

        int queryCount = queries.size();
        vector<int> queryResults(queryCount);
        for (int i = 0; i < queryCount; i++) {
            queryResults[i] = maxHeightAfterRemoval[queries[i]];
        }

        return queryResults;
    }

private:
    void traverseLeftToRight(TreeNode* node, int currentHeight) {
        if (node == nullptr)
            return;

        maxHeightAfterRemoval[node->val] = currentMaxHeight;
        currentMaxHeight = max(currentMaxHeight, currentHeight);
        traverseLeftToRight(node->left, currentHeight + 1);
        traverseLeftToRight(node->right, currentHeight + 1);
    }

    void traverseRightToLeft(TreeNode* node, int currentHeight) {
        if (node == nullptr)
            return;

        maxHeightAfterRemoval[node->val] = max(maxHeightAfterRemoval[node->val], currentMaxHeight);
        currentMaxHeight = max(currentHeight, currentMaxHeight);
        traverseRightToLeft(node->right, currentHeight + 1);
        traverseRightToLeft(node->left, currentHeight + 1);
    }
};

Complexity Analysis

| Algorithm                                                                                            | Time Complexity | Space Complexity |
| ---------------------------------------------------------------------------------------------------- | --------------- | ---------------- |
| Depth-First Search traversal with a post-order and then a post-order with a reverse hierarchy access | O(n)            | O(n)             |

Explanation

1. Intuition

• The problem requires finding the height of a binary tree after removing a subtree rooted at a given node.
• To solve this, we can use a two-pass approach: one pass from left to right and another from right to left.
• During the left-to-right pass, we update the maximum height of the tree after removing each node.
• During the right-to-left pass, we update the maximum height of the tree after removing each node, considering the maximum height of the right subtree.
• This approach ensures that we consider all possible removals and their effects on the tree height.
• By using this two-pass approach, we can efficiently calculate the height of the tree after removing each node.
• This solution works because it considers all possible removals and their effects on the tree height.

2. Implementation

• We start by initializing a vector maxHeightAfterRemoval to store the maximum height of the tree after removing each node.
• We define two helper functions: traverseLeftToRight and traverseRightToLeft, to perform the two passes.
• In traverseLeftToRight, we update maxHeightAfterRemoval with the current maximum height and recursively traverse the left and right subtrees.
• In traverseRightToLeft, we update maxHeightAfterRemoval with the maximum of the current value and the current maximum height, and recursively traverse the right and left subtrees.
• We use currentMaxHeight to keep track of the maximum height of the tree after removing each node.
• We iterate over the queries and return the corresponding values from maxHeightAfterRemoval.
• We use max to update currentMaxHeight and maxHeightAfterRemoval with the maximum values.

Complexity Analysis

Time Complexity:

• The given algorithm performs two depth-first search (DFS) traversals: traverseLeftToRight and traverseRightToLeft, each visiting every node in the binary tree exactly once.
• Within each traversal, the dominant operations are the recursive calls (traverseLeftToRight(node->left, currentHeight + 1) and traverseRightToLeft(node->right, currentHeight + 1)) and comparisons (max(currentMaxHeight, currentHeight) and max(maxHeightAfterRemoval[node->val], currentMaxHeight)). These operations occur once per node, resulting in a total of O(n) operations for all nodes combined.
• Given that both traversals visit every node once, and the operations within the traversals do not repeat, the time complexity is O(n), where n represents the number of nodes in the binary tree.

Space Complexity:

• The primary memory usage comes from the recursive call stack, which can reach a maximum depth of O(h), where h represents the height of the binary tree.
• However, due to the possibility that the binary tree can be skewed, representing an edge case where O(h) equals O(n), the maximum space complexity is O(n).
• Additional memory is used by the vectors (maxHeightAfterRemoval and queryResults), both having a fixed size. Nonetheless, the space complexity is dominated by the recursive call stack, maintaining an overall space complexity of O(n)

Footnote

This question is rated as Hard difficulty.

Hints

Try pre-computing the answer for each node from 1 to n, and answer each query in O(1).

The answers can be precomputed in a single tree traversal after computing the height of each subtree.

Similar Questions: