• Leetcode POTDs

Problem 2326 Spiral Matrix IV

Problem Statement

Link - Problem 2326

Question

You are given two integers m and n, which represent the dimensions of a matrix.

You are also given the head of a linked list of integers.

Generate an m x n matrix that contains the integers in the linked list presented in spiral order (clockwise), starting from the top-left of the matrix. If there are remaining empty spaces, fill them with -1.

Return the generated matrix.

Example 1

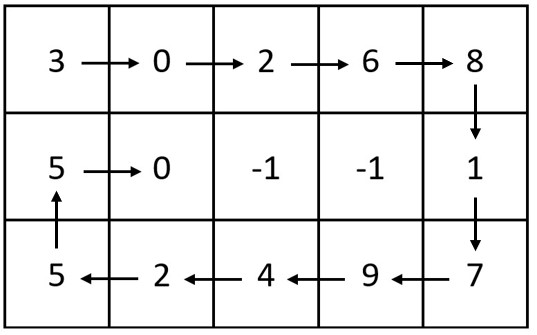
Input: m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
Output: [[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
Explanation: The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.

Example 2

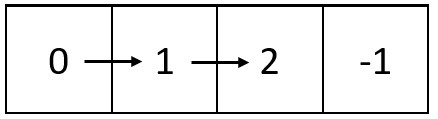
Input: m = 1, n = 4, head = [0,1,2]
Output: [[0,1,2,-1]]
Explanation: The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1

Constraints

• 1 <= m, n <= 10⁵
• 1 <= m * n <= 10⁵
• The number of nodes in the linked list is in the range [1, m*n].
• 0 <= Node.val <= 10⁵

Solution

class Solution
{
public:
    vector<vector<int>> spiralMatrix(int m, int n, ListNode *head)
    {
        vector<vector<int>> v(m, vector<int>(n, -1));

        ListNode *temp = head;
        int l, r, t, b;
        l = 0, r = n - 1, t = 0, b = m - 1;

        while (temp != nullptr)
        {
            for (int j = l; j <= r && temp != nullptr; j++)
            {
                int val = temp->val;
                v[t][j] = val;
                temp = temp->next;
            }
            t++;
            for (int i = t; i <= b && temp != nullptr; i++)
            {
                int val = temp->val;
                v[i][r] = val;
                temp = temp->next;
            }
            r--;
            for (int j = r; j >= l && temp != nullptr; j--)
            {
                int val = temp->val;
                v[b][j] = val;
                temp = temp->next;
            }
            b--;
            for (int i = b; i >= t && temp != nullptr; i--)
            {
                int val = temp->val;
                v[i][l] = val;
                temp = temp->next;
            }
            l++;
        }

        return v;
    }
};

Complexity Analysis

| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| Traverse  | O(mn)           | O(mn)            |

Explanation

1. Intuition

Let’s breakdown the requirements of the problem:

1. We need to generate an m x n matrix.
2. The matrix should contain the integers in the linked list presented in spiral order (clockwise).
3. If there are remaining empty spaces, fill them with -1.

To tackle the filling of -1 we can initialize the matrix with -1 values. Now the spiral order traversal

• We can start from the top-left corner of the matrix and move right.
• Once we reach the end of the row, we move down until we reach the bottom right which is not yet traversed.
• Then we move left until we reach bottom left which is not yet traversed.
• Finally, we move up until we reach the top left which is not yet traversed.

That means we need 4 variable to keep track of the cordinates that are not yet traversed. lets call them l (left), r (right), t (top), b (bottom).

• l,r will keep track of column traversal.
• t,b will keep track of row traversal.
• Hence initially l=0, r=n-1, t=0, b=m-1.
• Now first move from l to r and increment t. indicating that the top row is traversed.
• Then move from t to b and decrement r. indicating that the right column is traversed.
• Then move from r to l and decrement b. indicating that the bottom row is traversed.
• Finally move from b to t and increment l. indicating that the left column is traversed.
• Repeat the above steps until the linked list is completely traversed.

2. Implementation

- Initialize `temp` with the head of the linked list.
- Initialize a 2D vector `v` of size `m x n` with `-1` values.
- Initialize `l=0`, `r=n-1`, `t=0`, `b=m-1`.
- Traverse the linked list until `temp` is not `nullptr`.
  - Traverse from `l` to `r`
    - Assign the value of `temp->val` to `v[t][j]`.
    - Move `temp` to the next node.
  - Increment `t`.
  - Traverse from `t` to `b`
    - Assign the value of `temp->val` to `v[i][r]`.
    - Move `temp` to the next node.
  - Decrement `r`.
  - Traverse from `r` to `l`
    - Assign the value of `temp->val` to `v[b][j]`.
    - Move `temp` to the next node.
  - Decrement `b`.
  - Traverse from `b` to `t`
    - Assign the value of `temp->val` to `v[i][l]`.
    - Move `temp` to the next node.
  - Increment `l`.
- Return the 2D vector `v`.