Problem 2054 Two Best Non-Overlapping Events
Table of Contents
Problem Statement
Link - Problem 2054
Question
You are given a 0-indexed 2D integer array of events where events[i] = [startTimei, endTimei, valuei]. The ith event starts at startTimei and ends at endTimei, and if you attend this event, you will receive a value of valuei. You can choose at most two non-overlapping events to attend such that the sum of their values is maximized.
Return this maximum sum.
Note that the start time and end time is inclusive: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time t, the next event must start at or after t + 1.
Example 1:
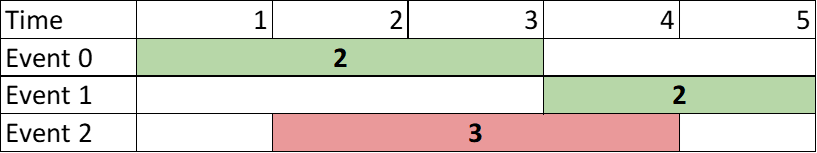
Input: events = [[1,3,2],[4,5,2],[2,4,3]] Output: 4 Explanation: Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.
Example 2:

Input: events = [[1,3,2],[4,5,2],[1,5,5]] Output: 5 Explanation: Choose event 2 for a sum of 5.
Example 3:

Input: events = [[1,5,3],[1,5,1],[6,6,5]] Output: 8 Explanation: Choose events 0 and 2 for a sum of 3 + 5 = 8.
Constraints:
2 <= events.length <= 105events[i].length == 31 <= startTimei <= endTimei <= 1091 <= valuei <= 106
Solution
class Solution {
public:
int maxTwoEvents(vector<vector<int>>& events) {
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq;
sort(events.begin(),events.end());
int max_val = 0, max_sum = 0;
for(auto event:events){
while(!pq.empty() && pq.top().first<event[0]){
max_val = max(max_val,pq.top().second);
pq.pop();
}
max_sum = max(max_sum,max_val+event[2]);
pq.push({event[1],event[2]});
}
return max_sum;
}
};
Complexity Analysis
| Algorithm | Time Complexity | Space Complexity |
| ------------------------ | --------------- | ---------------- |
| Priority Queue + Sorting | O(n log n) | O(n) |
Explanation
Intial Thoughts
This is a problem involving scheduling and maximizing value. I think about how to prioritize and organize events to maximize the sum of values from the chosen events. A priority queue could come in handy here to keep track of events. Additionally, sorting events by start time could help in identifying potential events to choose. Thinking about using variables to track maximum values and maximum sums could also be beneficial.
Intuitive Analysis
Imagine going through a calendar where you can attend at most two non-overlapping events. My approach is to have a flow where I continuously assess every upcoming event and evaluate the potential maximum sum it can contribute to. During the iteration, the events are sorted so I can consider one by one from the start. Also, maintaining a variable to remember the best value (maximum sum so far) helps in understanding when to consider updating that value. By keeping track of past events that could potentially contribute to a higher maximum sum, updating that best sum if encountered and verifying through comparison when an even greater sum becomes possible, is key to solving this kind of problems.
1. Intuition
- The problem can be solved by maintaining a priority queue of events that have ended.
- We sort the events by their start time to ensure we process them in order.
- We keep track of the maximum value of events that have ended so far.
- For each event, we remove all events from the priority queue that have ended before it starts.
- We update the maximum value if the top of the priority queue has a higher value.
- We add the current event to the priority queue and update the maximum sum.
- The maximum sum is the maximum value of the current event plus the maximum value of events that have ended.
2. Implementation
- We use a priority queue
pqto store events that have ended, wherepqis a min-heap of pairs(endTime, value). - We sort the
eventsvector by their start time usingsort(events.begin(), events.end()). - We initialize
max_valto 0 to keep track of the maximum value of events that have ended. - We iterate over the sorted
eventsvector and for each event, we remove all events frompqthat have ended before it starts usingwhile (!pq.empty() && pq.top().first < event[0]). - We update
max_valto be the maximum of its current value and the value of the top event inpqusingmax_val = max(max_val, pq.top().second). - We add the current event to
pqusingpq.push({event[1], event[2]}). - We update
max_sumto be the maximum of its current value and the sum ofmax_valand the value of the current event usingmax_sum = max(max_sum, max_val + event[2]).
Complexity Analysis
Time Complexity:
- The algorithm first sorts the events, which has a time complexity of O(n log n) due to the use of the built-in sort function.
- Then, it iterates over all events, and for each event, it pops elements from the priority queue until the top element’s end time is greater than or equal to the current event’s start time. This operation has a time complexity of O(log n) per event, resulting in a total of O(n log n) for all events.
- The overall time complexity is thus O(n log n) + O(n log n) = O(n log n), dominated by the sorting and priority queue operations.
Space Complexity:
- The algorithm uses a priority queue to store events, which has a maximum size of O(n) at any given time, since all events could potentially be in the queue.
- Additionally, the input vector of events has a size of O(n), which is not included in the space complexity because it is part of the input.
- Therefore, the overall space complexity is O(n) due to the priority queue.
Footnote
This question is rated as Medium difficulty.
Hints
How can sorting the events on the basis of their start times help? How about end times?
How can we quickly get the maximum score of an interval not intersecting with the interval we chose?
Similar Questions:
| Title | URL | Difficulty |
|---|---|---|
| Maximum Profit in Job Scheduling | https://leetcode.com/problems/maximum-profit-in-job-scheduling | Hard |
| Maximum Number of Events That Can Be Attended II | https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended-ii | Hard |
| Maximize Win From Two Segments | https://leetcode.com/problems/maximize-win-from-two-segments | Medium |