Leetcode POTDs

Problem 1905 Count Sub Islands

Posted on Aug 28, 2024 4 mins

Table of Contents

Problem Statement

Link - Problem 1905

Question

You are given two m x n binary matrices grid1 and grid2 containing only 0’s (representing water) and 1’s (representing land). An island is a group of 1’s connected 4-directionally (horizontal or vertical). Any cells outside of the grid are considered water cells.

An island in grid2 is considered a sub-island if there is an island in grid1 that contains all the cells that make up this island in grid2.

Return the number of islands in grid2 that are considered sub-islands.

Example 1

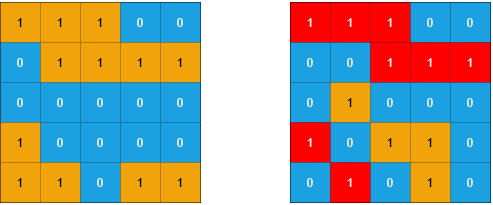
Input: grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]],
       grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
Output: 3
Explanation: In the picture above,
the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island.
 There are three sub-islands.

Example 2

Input: grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]],
       grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
Output: 2
Explanation: The grid on the left is grid1 and the grid on the right is grid2.
There are two sub-islands.

Constraints

- `m == grid1.length == grid2.length`
- `n == grid1[i].length == grid2[i].length`
- `1 <= m, n <= 500`
- `grid1[i][j] and grid2[i][j] are either 0 or 1.`

Solution

class Solution {
public:
    bool dfs(int i, int j, vector<vector<int>>& grid1, vector<vector<int>>& grid2, int n, int m) {
        if(i < 0 || j < 0 || i >= n || j >= m)
            return true;

        if(grid2[i][j] == 0)
            return true;
        grid2[i][j] = 0;

        bool isSubIsland = true;
        if(grid1[i][j] == 0)
            isSubIsland = false;

        bool right = dfs(i + 1, j, grid1, grid2, n, m);
        bool down = dfs(i, j + 1, grid1, grid2, n, m);
        bool left = dfs(i - 1, j, grid1, grid2, n, m);
        bool up = dfs(i, j - 1, grid1, grid2, n, m);

        return isSubIsland && right && down && left && up;
    }

    int countSubIslands(vector<vector<int>>& grid1, vector<vector<int>>& grid2) {
        int n = grid1.size();
        int m = grid1[0].size();

        int count = 0;
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                if(grid2[i][j] == 1) {
                    if(dfs(i, j, grid1, grid2, n, m)) {
                        count++;
                    }
                }
            }
        }
        return count;
    }
};

Complexity Analysis

| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| DFS       | O(NM)           | O(NM)            |

Explanation

1. Intuition

So lets take a moment to summarize the problem statement and build up intuition.

We need to find all the islands in grid2.
Check whether each island in grid2 is covered by an island in grid1.
So to a cover is generated when the island in grid1 is atleast as same as the island in grid2.
That means we can say an island in grid2 is covered if all the corresponding cells in grid1 are 1.
Even if a single cell is not same inside the islands on grids then its not covered.
So that being said, Now we can observe that we need to find all the possible islands and then check if the corresponding cells are same in grid1 and grid2.
To find all the islands we can use DFS as the classic island count problem.

- We can count the number of islands in `grid2` using DFS.
- First check if the co-ordinates are valid
- Then check if the cell is water or not
  - If water then return
  - If not then mark the cell as water ( means visited )
- Then check if the cell is land in `grid1`
  - If not then its not a sub island
  - If yes then its a sub island
- Then recursively check for all the 4 directions

2. Implementation

- Define a `boolean` function `dfs`
- Inputs are `i`, `j`, `grid1`, `grid2`, `n`, `m`
- `i` is the row index, `j` is the column index
- `grid1` and `grid2` are the 2D vectors
- `n` and `m` are the dimensions of the grid
- If the co-ordinates are out of bounds then return `true`
- If the cell is water then return `true`
- Mark the cell as water
- Initialize `isSubIsland` as `true`
- Check if the cell is land in `grid1`
  - If not then `isSubIsland` is `false`
- Recursively check for all the 4 directions
- `right`, `down`, `left`, `up` are the recursive calls
- return `isSubIsland && right && down && left && up`
- This represents if the current cell contributes to the sub island or not

Similar question Problem 200 classic islands

Solution to Problem 200 classic islands