• Leetcode POTDs

Problem 1861 Rotating the Box

Problem Statement

Link - Problem 1861

Question

You are given an m x n matrix of characters box representing a side-view of a box. Each cell of the box is one of the following:

• A stone '#'
• A stationary obstacle '*'
• Empty '.'

The box is rotated 90 degrees clockwise, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity does not affect the obstacles' positions, and the inertia from the box's rotation does not affect the stones' horizontal positions.

It is guaranteed that each stone in box rests on an obstacle, another stone, or the bottom of the box.

Return an n x m matrix representing the box after the rotation described above.

Example 1:

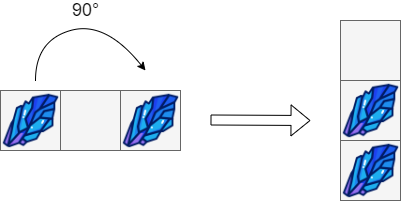
Input: box = [["#",".","#"]]
Output: [["."],
         ["#"],
         ["#"]]

Example 2:

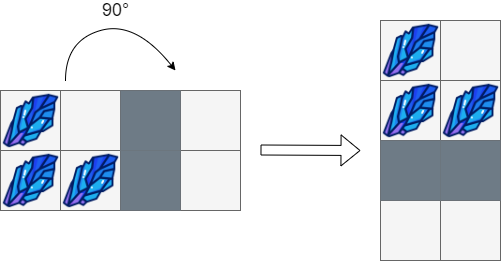
Input: box = [["#",".","*","."],
              ["#","#","*","."]]
Output: [["#","."],
         ["#","#"],
         ["*","*"],
         [".","."]]

Example 3:

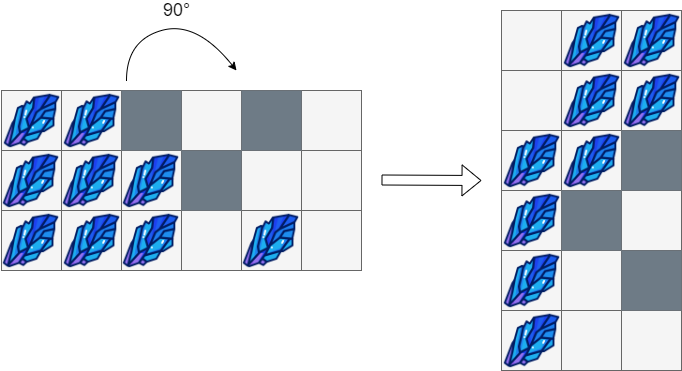
Input: box = [["#","#","*",".","*","."],
              ["#","#","#","*",".","."],
              ["#","#","#",".","#","."]]
Output: [[".","#","#"],
         [".","#","#"],
         ["#","#","*"],
         ["#","*","."],
         ["#",".","*"],
         ["#",".","."]]

Constraints:

• m == box.length
• n == box[i].length
• 1 <= m, n <= 500
• box[i][j] is either '#', '*', or '.'.

Solution

class Solution {
public:
    vector<vector<char>> rotateTheBox(vector<vector<char>>& box) {
        int m =box.size(),n=box[0].size();
        for(auto &row:box){
            int obstacle = row.size();
            for(int i = row.size()-1; i>=0; i--){
                if(row[i]=='#'){
                    char temp = row[i];
                    row[i]='.';
                    row[obstacle-1]=temp;
                    obstacle--;
                }

                if(row[i]=='*')
                    obstacle =i;
            }
        }

        vector<vector<char>>result(n,vector<char>(m,'.'));

        for(int i = 0; i<m; i++)
            for(int j = 0; j<n; j++)
                result[j][m-1-i] = box[i][j];

        return result;
    }
};

Complexity Analysis

| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| Greedy    | O(mn)           | O(mn)            |

Explanation

1. Intuition

- The problem requires us to simulate the rotation of a box 90 degrees clockwise and let the stones fall due to gravity.
- We can solve this problem in two steps: first, we simulate the falling of stones in each row, and then we rotate the box 90 degrees clockwise.
- To simulate the falling of stones, we iterate over each row from right to left and move the stones to the rightmost available position.
- If we encounter an obstacle, we move the obstacle to its original position and continue the process.
- After simulating the falling of stones, we rotate the box 90 degrees clockwise by swapping the rows and columns.

2. Implementation

• We start by iterating over each row in the box and simulating the falling of stones.
• We use a variable obstacle to keep track of the rightmost available position in the row.
• We iterate over each character in the row from right to left and check if it is a stone.
• If it is a stone, we move it to the rightmost available position by swapping it with the character at the obstacle index.
• We then decrement the obstacle index to keep track of the new rightmost available position.
• If we encounter an obstacle, we move it to its original position and reset the obstacle index.
• After simulating the falling of stones, we create a new matrix result to store the rotated box.
• We iterate over each character in the original box and assign it to the corresponding position in the result matrix.
• We use the formula result[j][m-1-i] = box[i][j] to rotate the box 90 degrees clockwise.
• Finally, we return the result matrix.

Complexity Analysis

Time Complexity:

• Two nested loops are used to iterate through the box, each loop runs in O(m) and O(n) time respectively, where m is the number of rows and n is the number of columns.
• Inside the loops, constant time operations are performed, so they don’t affect the overall time complexity.
• Therefore, the overall time complexity is O(mn) due to the nested loops.

Space Complexity:

• A new 2D vector is created to store the result, which requires O(mn) space.
• The input 2D vector is also stored in memory, but this is not included in the space complexity because it is part of the input, not the auxiliary space used by the algorithm.