The Indian Engineer

Problem 1514 Path With Maximum Probability

Posted on 3 mins

Dijkstra Graph

Table of Contents

Problem Statement

Link - Problem 1514

Question

You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].

Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.

Example 1

img1 

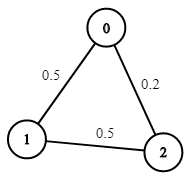
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

Example 2

img2 

Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
Output: 0.30000

Example 3

img3 

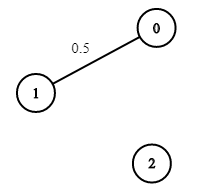
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
Output: 0.00000
Explanation: There is no path between 0 and 2.

Constraints

Solution 

class Solution {
public:
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        vector<double>prob(n,0.0);
        prob[start]= 1.0;
        vector<vector<pair<double,int>>>adj(n);
        for(int i = 0; i<edges.size(); i++){
            adj[edges[i][0]].push_back({succProb[i],edges[i][1]});
            adj[edges[i][1]].push_back({succProb[i],edges[i][0]});
        }

        priority_queue<pair<double,int>,vector<pair<double,int>>>pq;

        pq.push({1.0,start});

        while(!pq.empty()){
            auto [curr,i] = pq.top();
            pq.pop();

            if(i == end)
                return curr;

            for(auto [nextprob,j]:adj[i]){
                double newprob = curr*nextprob;
                if(newprob>prob[j]){
                    prob[j] = newprob;
                    pq.push({newprob,j});
                }
            }
        }

        return 0.0;
    }
};

Complexity Analysis 

| Algorithm | Time Complexity | Space Complexity |
| --------- | --------------- | ---------------- |
| Dijkstra  | O(ElogV)        | O(V+E)           |

Explanation

1. Intuition 

- We can use Dijkstra's algorithm to find the path with maximum probability.
- But to make it work we need to store the maximum probabilty of reaching a node
  from the start node.

It’s known that

\[P(A \cap B) = P(A \mid B) \times P(B)\]

Let \(B\) denote the set for a path to the current vertex.

Let \(A\) denote the set for paths to the next vertex.

So \(A \cap B\) is the set for a path passing the current vertex and the next vertex.

Let \(P(B)\) denote the probability to the current vertex.

Let \(P(A \mid B)\) denote the probability from the current vertex to the next vertex.

Then \(P(A \cap B)\) is the probability of the path passing the current vertex and then the next vertex.

2. Implementation 

- Intialize a vector `prob` to store the maximum probability of reaching a node from the `start` node.
- Intialize a vector of vectors `adj` to store the adjacency list of the graph.
- Iterate over the edges and store the adjacency list.
- Intialize a priority queue `pq` to store the maximum probability and the node.
- Push the start node with probability 1.0 into the priority queue.
- While the priority queue is not empty:
  - Pop the top element from the priority queue.
  - If the node is the end node, return the probability.
  - Iterate over the adjacency list of the node:
    - Calculate the new probability.
    - If the new probability is greater than the previous probability:
      - Update the probability.
      - Push the new probability and the node into the priority queue.
- Return 0.0 if there is no path.